Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ giả thiết ta suy ra tam giác ABC là tam giác vuông cân tại B
Thể tích của khối lăng trụ là \(V_{ABC.A'B'C'}=AA'.BC=a\sqrt{2.}\frac{1}{2}a^2=\frac{\sqrt{2}}{2}a^3\)
Gọi E là trung điểm của BB'. Khi đó mặt phẳng (AME) song song với B'C nên khoảng cách giữa 2 đường thẳng AM, B'C bằng khoảng cách giữa B'C và mặt phẳng (AME)
Nhận thấy, khoảng cách từ B đến mặt phẳng (AME) bằng khoảng cách từ C đến mặt phẳng (AME)
Gọi h là khoảng cách từ B đến mặt phẳng (AME). Do đó tứ diện BAME có BA, BM, BE đôi một vuông góc với nhau nên :
\(\frac{1}{h^2}=\frac{1}{BA^2}+\frac{1}{BM^2}+\frac{1}{BE^2}\Rightarrow\frac{1}{h^2}=\frac{1}{a^2}+\frac{4}{a^2}+\frac{2}{a^2}=\frac{7}{a^2}\)
\(\Rightarrow h=\frac{a\sqrt{7}}{7}\)
Vậy khoảng cách giữa 2 đường thẳng B'C và AM bằng \(\frac{a\sqrt{7}}{7}\)

Đáp án C.
Hướng dẫn giải:
Ta có
![]()
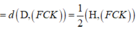
Kẻ H I ⊥ C K , H J ⊥ F I
![]()
Ta có H I = 2 a 5 5
![]()
⇒ S B = a 3
![]()
⇒ H F = a 2 2
Ta có 1 H J 2 = 1 H I 2 + 1 H F 2 = 13 4 a 2
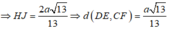

Đáp án: D.
Hướng dẫn giải:
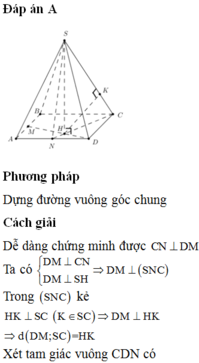
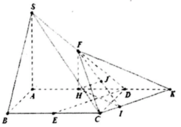
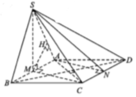
O = A C ∩ B D , Gọi , I là trung điểm cạnh đáy BC.
Vì SA = SB = SC = SD nên S O ⊥ ( A B C D )
Từ đó ta chứng mình được B C ⊥ ( S O I )
⇒ O H ⊥ ( S B C ) (với O H ⊥ B C tại SI).
Do E F / / ( S B C ) S K ⊂ ( S B C )
nên d(EF,SK) = d(EF,(SBC)) = OH.
Thực hiện tính toàn để được
O C = 1 2 A C = a 5 2 ⇒ S O = a 3 2
Kết luận:

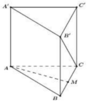
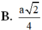
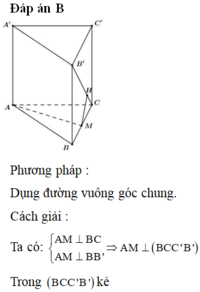

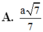
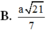
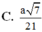
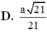


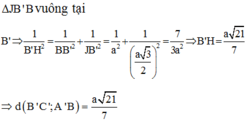
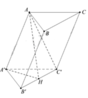

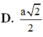
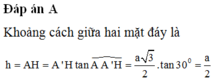
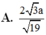
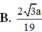
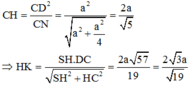
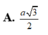
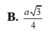
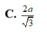
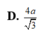
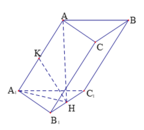


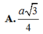
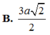
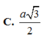
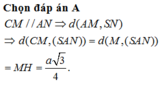
Gọi (\(\alpha\)) là mặt phẳng chứa DE và song song với \(A_1F\) thì khoảng cách cần tính bằng khoảng cách từ F đến ( \(\alpha\))
Theo giả thiết suy ra lăng trụ đã cho là lăng trụ đứng có đáy là tam giác đều cạnh a
Gọi K là trung điểm của \(FC_1\) thì \(EK\)//\(A_1F\)//AD, suy ra (\(\alpha\)) \(\equiv\left(ADKE\right)\)
Ta có \(A_1F\perp B_1C_1\Rightarrow A_1F\perp\left(BCC_1B_1\right)\) \(\Rightarrow EK\perp\left(BCC_1B_1\right)\)
Gọi H là hình chiếu vuông góc của F lên đường thẳng DK thì \(FH\perp\left(ADKE\right)\) suy ra FH là khoảng cách cần tính
Trong tam giác vuông DKF, ta có :
\(\frac{1}{FH^2}=\frac{1}{FD^2}+\frac{1}{FK^2}=\frac{1}{\left(\frac{a}{4}\right)^2}\Rightarrow FH=\frac{a}{\sqrt{17}}\)
a