Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B1: Chứng minh AM, BN, CP chia tam giác ABC thành 6 tam giác có diện tích bằng nhau.
B2:
=> S( AOB) =2/3 S(ANB) => OB = 2/3 BN
S(AOC) =2/3 S(ACP) => OC =2/3 CP
S(AOB) = 2/3 S(AMB) => OA = 2/3 AM
B3: kết luận

Bài này lên cấp 2 sẽ gọi là trọng tâm, giao điểm 3 đường trung tuyến.
Ta có: M trung điểm BC, N trung điểm AC. 2 đoạn này cắt nhau tại H.
CH cắt AB tại P.
Gọi D đối xứng H qua M, E đối xứng H qua N.
Chứng minh AECH, BDCH là các hình bình hành.
Chứng minhAEDB là hình bình hành => H t điểm EB EP//AE
=> P trung điểm AB
Câu sau dễ rồi.

Ta có S GMB = S GMC(vì MB=MC,chung chiều cao hạ từ G) (1)
S GNC=S GNA(vì NA=NC,chung chiều cao hạ từ G) (2)
Lại có:S BCN=1/2 S ABC (2 tam giác có chung chiều cao hạ từ B và đáy CN=1/2 CA)
S ACM=1/2 S ABC (2 tam giác có chung chiều cao hạ từ A và đáy CM=1/2 CB)
=>S BCN=S ACM
Mà S ACM và S BCN cùng có chung S GCM+S GCN
=>S GMB=S GNA (3)
Từ (1),(2),(3) ta có:
S GMC=S GNC=S GNA hay S GMC=1/3(S GMC+S GNC+S GNA)
=>S GMC=1/3 S CMA,hay GM=1/3AM (2 tam giác CMA và CMG có chung chiều cao hạ từ C)
Do đó,BN cắt AM tại G ở 1/3 của AM kể từ đáy.
(Tương tự ta chứng minh được CP cũng cắt AM tại G ở 1/3 của AM kể từ đáy)
Vậy ba đoạn AM,BN,CP cắt nhau ở một điểm G nằm ở 1/3 của mỗi đoạn kể từ đáy.

a) Vì AB = 3 x AM, AC = 3 x AN, nên MB = 2/3 x AB, NC = 2/3 x AC.
Từ đó suy ra : dt (MBC) = 2/3 x dt (ABC) (chung chiều cao từ C
dt (NCB) = 2/3 x dt (ABC) (chung chiều cao từ B)
Vậy dt (MBC) = dt (NCB) mà tam giác MBC và tam giác NCB có chung đáy BC, nên chiều cao từ M bằng chiều cao từ N xuống đáy BC hay MN song song với BC. Do đó BMNC là hình thang.
Từ MB = 2/3 x AB, nên dt (MBN) = 2/3 x dt (ABN) (chung chiều cao từ N) hay dt (ABN) = 2/3 x dt (MBN).
Hơn nữa từ AC = 3 x AN, nên NC = 2 x AN, do đó dt (NBC) = 2 x dt (ABN) (chung chiều cao từ B) ; suy ra dt (NBC) = 3/2 x 2 x dt (MBN) = 3 x dt (MBN).
Mà tam giác NBC và tam giác MBN có chiều cao bằng nhau (cùng là chiều cao của hình thang BMNC). Vì vậy đáy BC = 3 x MN.
b) Gọi BN cắt CM tại O. Ta sẽ chứng tỏ AI cũng cắt BN tại O. Muốn vậy, nối AO kéo dài cắt BC tại K, ta sẽ chứng tỏ K là điểm chính giữa của BC (hay K trùng với I).
Theo phần a) ta đã có dt (NBC) = 2 x dt (ABN). Mà tam giác NBC và tam giác ABN có chung đáy BN, nên chiều cao từ C gấp 2 lần chiều cao từ A xuống đáy BN. Nhưng đó là chiều cao tương ứng của hai tam giác BCO và BAO có chung đáy BO, vì vậy dt (BCO) = 2 x dt (BAO)
Tương tự ta cũng có dt (BCO) = 2 x dt (CAO).
Do đó dt (BAO) = dt (CAO). Hai tam giác BAO và CAO có chung đáy AO, nên chiều cao từ B bằng chiều cao từ C xuống đáy AO. Đó cũng là chiều cao tương ứng của hai tam giác BOK và COK có chung đáy OK, vì vậy dt (BOK) = dt (COK). Mà hai tam giác BOK và tam giác COK lại chung chiều cao từ O, nên hai đáy BK = CK hay K là điểm chính giữa của cạnh BC. Vậy điểm K trùng với điểm I hay BN, CM, AI cùng cắt nhau tại điểm O.

a) Vì AB = 3 x AM, AC = 3 x AN, nên MB = 2/3 x AB, NC = 2/3 x AC.
Từ đó suy ra : dt (MBC) = 2/3 x dt (ABC) (chung chiều cao từ C)
dt (NCB) = 2/3 x dt (ABC) (chung chiều cao từ B)
Vậy dt (MBC) = dt (NCB) mà tam giác MBC và tam giác NCB có chung đáy BC, nên chiều cao từ M bằng chiều cao từ N xuống đáy BC hay MN song song với BC. Do đó BMNC là hình thang.
Từ MB = 2/3 x AB, nên dt (MBN) = 2/3 x dt (ABN) (chung chiều cao từ N) hay dt (ABN) = 2/3 x dt (MBN).
Hơn nữa từ AC = 3 x AN, nên NC = 2 x AN, do đó dt (NBC) = 2 x dt (ABN) (chung chiều cao từ B) ; suy ra dt (NBC) = 3/2 x 2 x dt (MBN) = 3 x dt (MBN).
Mà tam giác NBC và tam giác MBN có chiều cao bằng nhau (cùng là chiều cao của hình thang BMNC). Vì vậy đáy BC = 3 x MN.
b) Gọi BN cắt CM tại O. Ta sẽ chứng tỏ AI cũng cắt BN tại O. Muốn vậy, nối AO kéo dài cắt BC tại K, ta sẽ chứng tỏ K là điểm chính giữa của BC (hay K trùng với I).
Theo phần a) ta đã có dt (NBC) = 2 x dt (ABN). Mà tam giác NBC và tam giác ABN có chung đáy BN, nên chiều cao từ C gấp 2 lần chiều cao từ A xuống đáy BN. Nhưng đó là chiều cao tương ứng của hai tam giác BCO và BAO có chung đáy BO, vì vậy dt (BCO) = 2 x dt (BAO)
Tương tự ta cũng có dt (BCO) = 2 x dt (CAO).
Do đó dt (BAO) = dt (CAO). Hai tam giác BAO và CAO có chung đáy AO, nên chiều cao từ B bằng chiều cao từ C xuống đáy AO. Đó cũng là chiều cao tương ứng của hai tam giác BOK và COK có chung đáy OK, vì vậy dt (BOK) = dt (COK). Mà hai tam giác BOK và tam giác COK lại chung chiều cao từ O, nên hai đáy BK = CK hay K là điểm chính giữa của cạnh BC. Vậy điểm K trùng với điểm I hay BN, CM, AI cùng cắt nhau tại điểm O.

Vì là giao của 3 đường trung tuyến
=> O là trọng tâm
=> AO/AN=2/3
=> ON/AN=1/3
ABC và OBC có chung cạnh đáy
Tỉ số chiều cao =ON/AN=1/3 => Tỉ số S = 1/3 => S.OBC=1/3.S.ABC ( Thay số vào là ra)=216
Đoạn Tỉ số đường cao = ON/AN phải kẻ đường cao và CM nhé
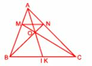
B1: Chứng minh AM, BN, CP chia tam giác ABC thành 6 tam giác có diện tích bằng nhau. B2: => S( AOB) =2/3 S(ANB) => OB = 2/3 BN S(AOC) =2/3 S(ACP) => OC =2/3 CP S(AOB) = 2/3 S(AMB) => OA = 2/3 AM B3: kết luận