Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dòng điện qua mạch:
\(I=\dfrac{\xi}{r+R}=\dfrac{12}{2+R}\)
Công suất nguồn:
\(P=\xi\cdot I=12\cdot\dfrac{12}{2+R}=24W\)
\(\Rightarrow R=4\Omega\)
Chọn D.

Dòng điện qua mạch:
\(I=\dfrac{\xi}{r+R}=\dfrac{12}{2+4}=2A\)
Công suất nguồn:
\(P=\xi\cdot I=12\cdot2=24W\)
Chọn C.

Đáp án: B
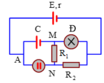
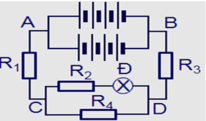
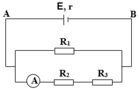
HD Giải: I1 = 1/3 A, U2 = U1 = I1R1 = 12/3 = 4V, I 2 = U 2 R 2 = 4 6 = 2 3 A , I3 = I = I1 + I2 = 1A
UN = E – Ir = 8 – 1 =7V, U3 = UN – U1 = 7 – 4 = 3V, Q3 = U3I3t = 3.1.(10.60) = 1800 J = 1,8kJ

Đáp án: B
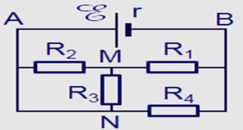
HD Giải: I2 = I3 = I23 = 1,5A, R23 = 6+4 = 10W,
U1 = U23 = I23R23 = 1,5.10 = 15V, I 1 = U 1 R 1 = 15 15 = 1 A , I = I1 + I23 = 1 + 1,5 = 2,5A
1 R N = 1 15 + 1 10 = 1 6 ⇒ R N = 6 Ω , A = EIt = I2(RN + r)t = 2,52(6 + 2).(15.60) = 45000J = 45 kJ

Đáp án D
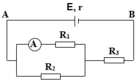
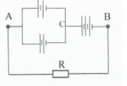
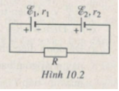
Theo sơ đồ hình 10.2 thì hai nguồn này tạo thành bộ nguồn nối tiếp, do đó áp dụng định luật Ôm cho toàn mạch ta tìm được dòng điện chạy trong mach có cường độ là :
I = 4/(R + 0,6)
Giả sử hiệu điện thế giữa hai cực của nguồn E 1 bằng 0, ta có
U 1 = E 1 - I r 1 = 2 - 1,6/(R+0,6) = 0
Phương trình này cho nghiệm là : R = 0,2 Ω
Giả sử hiệu điện thế giữa hai cực của nguồn E 2 bằng 0 ta có U 2 = E 2 – I r 2
Thay các trị số ta cũng đi tới một phương trình của R. Nhưng nghiệm của phương trình này là R = -0,2 Ω < 0 và bị loại.
Vậy chỉ có một nghiệm là : R = 0,2 Ω và khi đó hiệu điện thế giữa hai cực của nguồn bằng 0.

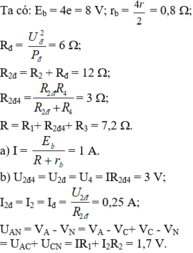


Đáp án cần chọn là: D
Ta có cường độ dòng điện I=0,6A(Tính được ở các câu trên)
Þ Công của nguồn điện sản ra trong 5 phút:
A = E I t = 6.0 , 6.5.60 = 1080 J