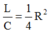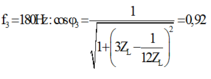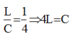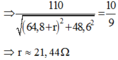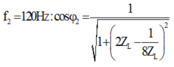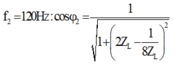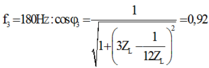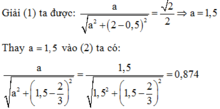Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giải thích: Đáp án D
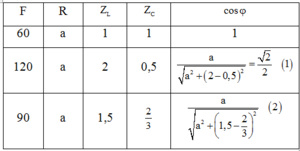
Theo đề bài, ta có:
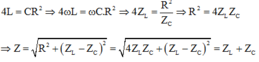
Hệ số công suất trong mạch: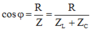 
Dùng phương pháp chuẩn hóa:
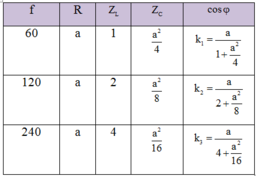
Theo đề bài:
. Khi tần số f = f3 = 180 Hz thì hệ số công suất của mạch gần với giá trị nào sau đây nhất ?
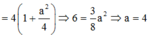
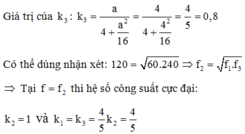
Đáp án D
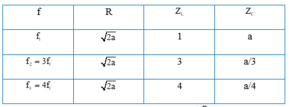
Ta chuẩn hóa số liệu:
+ f =
f
1
= 60 Hz: Đặt R = 1 thì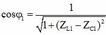 
+ f =
f
2
= 120 Hz: có 
+ f =
f
3
= 180 Hz: có
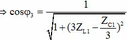
Theo đề bài: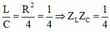 
Có 
Từ (1) và (2) tìm được 
Thay vào cos
φ
3
= 0,923
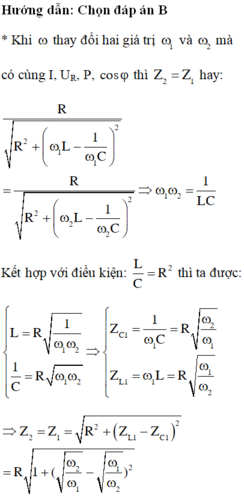
Chuẩn hóa R = 1 ⇒ L = C = X
Hai giá trị của tần số góc cho cùng giá trị công suất : ω 1 ω 2 = 1 L C = 1 X 2
Tần số góc để điện hấp hiệu dụng ở hai đầu cuộn cảm đạt cực đại: ω 3 2 = 1 L C − R 2 C 2 2 = 2 X 2
Ta có: cos φ = R R 2 + L ω 1 − 1 C ω 1 2 = 1 1 + X 2 ω 1 − ω 2 2
Mặc khác ω 1 = ω 2 + 2 ω 3 ⇒ ω 1 − ω 2 = 2 ω 3 = 2 X 2
Thay vào biểu thức trên ta thu được cos φ = 1 1 + 2 2 = 0 , 447
Đáp án B
Đáp án A
Phương pháp: Sử dụng các biến đổi toán học và bài toán f biến thiên
Cách giải: Ta có
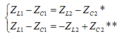
Xét **
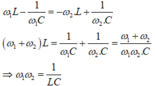
Tính toán tương tự ta loại * Khi thay đổi đến tần số f3 thì UL cực đại, khi đó
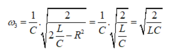
⇒ ω 1 . ω 2 = ω 2 3 2
Mà đề bài cho ta biết
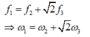
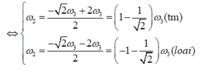
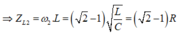
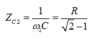
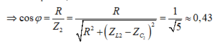
Đáp án C
Ban đầu mạch có tính cảm kháng 
-> Khi tăng
ω
thì
Z
L
càng tăng còn
Z
C
giảm đi, do đó tổng trở 
càng tăng
giảm đi. Chọn C.
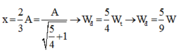. Chọn A.
Giả sử rằng ω 1 = n ω 2 .
Khi ω = ω 2 , mạch xảy ra cộng hưởng Z L 2 = Z C 2 , ta chuẩn hóa Z L 2 = Z C 2 = 1 .
Khi ω = ω 1 = n ω 2 ⇒ Z L = n Z C = 1 n , chú ý rằng lúc này mạch đang có tính cảm kháng do vậy n > 1.
Từ giả thuyết của bài toán ta có
cos φ A M = r r 2 + n 2 = 0 , 6 ⇒ r = 3 4 n
cos φ A B = r r 2 + n − 1 n 2 = 0 , 8 → r = 3 4 n 0 , 8 = 3 4 n 9 16 n 2 + n − 1 n 2 ⇒ n = 0 , 8 n = 4 7
Vậy ta tìm được f 2 = f 1 4 7 = 15 7 ≈ 40 Hz
Đáp án C