Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Kí hiệu như hình vẽ.
Ta thấy I K = r ' là bán kính đáy của hình chóp, A I = h là chiều cao của hình chóp.
Tam giác vuông tại K có IK là đường cao
⇒ I K 2 = A I . I M ⇒ r ' 2 = h . 2 r − h
Ta có V c o h p = 1 3 . π r ' 2 . h = 1 3 . π . h . h . 2 r − h = 4 3 π . h 2 . h 2 2 r − h .
Áp dụng bất đẳng thức Cauchy ta có
h 2 . h 2 . 2 r − h ≤ h 2 + h 2 + 2 r − h 3 27 = 8 r 3 27
⇔ V c h o p ≤ 4 3 π . 8 r 3 27 = 32 81 . π r 3
Dấu bằng xảy ra khi h 2 = 2 r − h ⇔ h = 4 r 3 . Vậy ta chọn A

Đáp án A
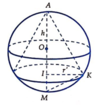
Kí hiệu bán kính đáy của hình nón là x, chiều cao hình nón là y (trong đó 0<x≤2R; 0<y≤R). Gọi SS’là đường kính của mặt cầu ngoại tiếp hình nón thì ta có:
![]() (hệ thức lượng trong tam giác vuông)
(hệ thức lượng trong tam giác vuông)
Gọi V1 là thể tích khối nón: 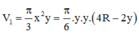
Mặt khác 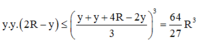
Do đó 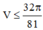 dấu bằng xảy ra
dấu bằng xảy ra ![]()
Khi đó 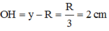

Đáp án A
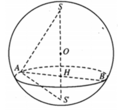
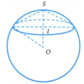
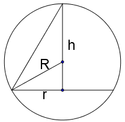
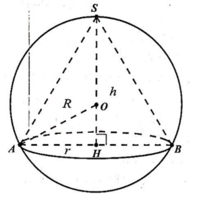
Theo bài ra, ta có khối nón (N) nội tiếp khối cầu (S).
Giả sử khối nón (N) có đỉnh A, tâm đáy I như hình vẽ bên với h = I A là chiều cao và bán kính đáy r = I K
Tam giác AMK vuông tại K, có I K 2 = I A . I M ⇔ r 2 = h 2 R − h
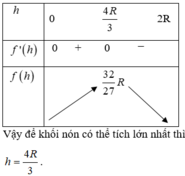
Suy ra V N = 1 3 π r 2 h = π 3 h 2 2 R − h = π 3 . 2 R h 2 − h 3
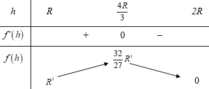
Xét hàm số f h = 2 R h 2 − h 3 trên khoảng 0 ; 2 R → max f h = 32 R 3 27
Vậy thể tích cần tính là V = π 3 . 32 R 3 27 = 32 π R 3 81

Chọn đáp án A
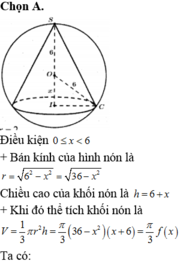
Gọi I là tâm của hình tròn (C) và S là đỉnh của hình nón. Gọi bán kính của hình tròn (C) là r thì
![]()
Trường hợp 1: O nằm giữa S và I.
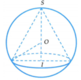
Chiều cao của hình chóp là SI = SO + OI = x + 6 (cm).
Thể tích khối chóp là V = 1 3 π 36 - x 2 x + 6 cm 3
Xét hàm số f x = 36 - x 2 x + 6 với 0 ≤ x < 6
Ta có f ' x = - 3 x 2 - 12 x + 36
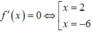
Do 0 ≤ x < 6 nên x = - 6.
Lập bảng biến thiên của hàm số ta thấy f(x) ta thấy f x ≤ f 2 = 256
Suy ra V ≤ V 1 = 1 3 π . 256 = 256 3 π cm 3
Dấu “=” xảy ra x = 2.
Trường hợp 2: I nằm giữa S và O
Chiều cao của hình chóp là SI = SO – OI = 6 – x (cm)
Thể tích của khối chóp là V = 1 3 π 36 - x 2 6 - x cm 3 (cm3).
Xét hàm số g x = 36 - x 2 6 - x với 0 ≤ x < 6
Ta có g ' x = 3 x 2 - 12 x - 36 < 0 , ∀ x ∈ 0 ; 6 nên hàm số g(x) nghịch biến trên 0 ; 6 .
Suy ra g x ≤ g 0 = 216
Khi đó V ≤ V 2 = 72 π cm 3 .
Dấu “=” xảy ra khi x = 0.
So sánh hai trường hợp 1 và 2, suy ra thể tích lớn nhất của khối chóp đã cho là V = 256 3 π cm 3 khi x = 2 c m .
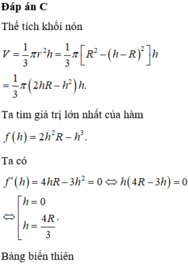

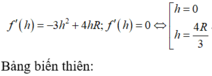
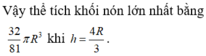
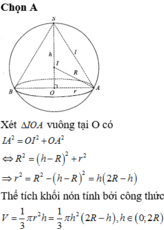
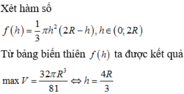
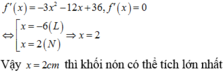
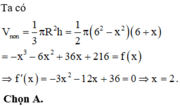
Đáp án D
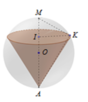
Kí hiệu như hình vẽ bên
Chuẩn hóa R = 1 và gọi r,h lầm lượt là bán kính đáy và chiều cao của hình nón
⇒ Thể tích khối nón là V 1 = 1 3 π r 2 h
Tam giác AMK vuông tại K, có:
I K 2 = I M . I A ⇔ r 2 = h 2 R − h = h 2 − h
Để V 1 V 2 lớn nhất ⇔ V 2 V 1 = V C − V 1 V 1 = V C V 1 − 1 nhỏ nhất ⇔ V 1 đạt giá trị lớn nhất
Khi đó V 1 = π 3 h 2 2 − h ≤ π 3 . 32 27 = 32 π 81 (khảo sát hàm số f h = 2 h 2 − h 3 ) )
Vậy tỉ số:
V 1 V 2 = 1 : V C V 1 − 1 = 1 : 4 π 3 : 32 π 81 − 1 = 8 19