Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\widehat{MON}=180^0-\widehat{MAN}=120^0\)
\(S=4\pi R^2=36\pi\Rightarrow R=3\Rightarrow OM=ON=3\)
Áp dụng định lý hàm cos cho tam giác MON:
\(MN=\sqrt{OM^2+ON^2-2OM.ON.cos\widehat{MON}}=\sqrt{3^2+3^2-2.3.3.cos120^0}=3\sqrt{3}\)

\(S=4\pi R^2=36\pi\Rightarrow R=3\) \(\Rightarrow OA=3\)
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\) và \(OH=2\sqrt{2}\)
Pitago tam giác vuông OAH:
\(AH=\sqrt{OA^2-OH^2}=1\)
\(\Rightarrow AB=2AH=2\)

\(S=4\pi R^2=36\pi\Rightarrow R=3\)
\(V=\dfrac{4}{3}\pi R^3=36\pi\)

Chọn A
Gọi I (a;b;c)
Ta có IA=IO=R ó hình chiếu của I lên OA là trung điểm 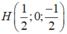 của OA.
của OA.
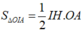
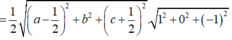
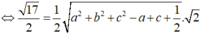
![]()
![]()
Theo bài ra ta có:
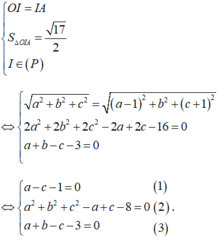
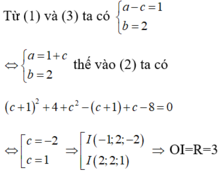

Đáp án A.
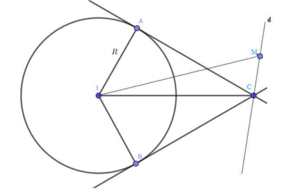
Phương pháp giải: Dựng hình, xác định tập hợp tiếp điểm
Lời giải:
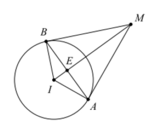
Xét mặt cầu ( S ) : x - 1 2 + y - 1 2 + z 2 = 0 có tâm I(1;1;0) bán kính R =2
![]()
Gọi A,B là các tiếp điểm. => E là tâm đường tròn (C), với bán kính r=EA (Hình vẽ bên).
Tam giác MAI vuông tại A, có
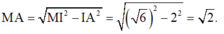
Suy ra
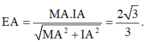
Vậy bán kính của (C) là r = 2 3 3

Đáp án là A
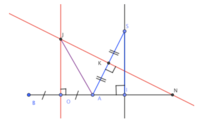
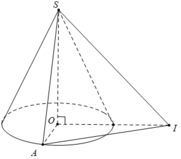
* Gọi J là tâm mặt cầu qua đường tròn tâm O và điểm S => J nằm trên đường trung trực của AB và SA
*Tam giác SIA vuông tại I.
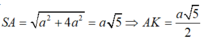
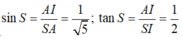
*Ta có: Góc N và S bằng nhau vì cùng phụ với góc S A N ^
* Tam giác AKN vuông tại K
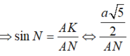
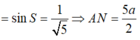
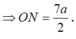
* Tam giác OJN vuông tại O
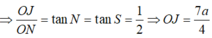
* Tam giác AOJ vuông tại O
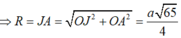
Cách 2
Gắn hệ trục toạ độ Oxy sao cho A, B, O thuộc tia Ox, S thuộc tia Oy và giả sử a = 1.
Khi đó A(1;0), B(3;0), S(0;2)
![]()
là đường tròn tâm J qua 3 điểm A, S, B
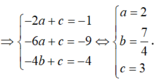
Suy ra:
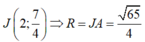
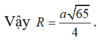
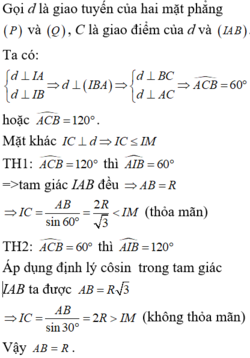




\(S=4\pi R^2=36\pi\Rightarrow R=3\)
\(\Rightarrow OB=R=3\)
Áp dụng định lý Pitago cho tam giác OAB:
\(AB=\sqrt{OA^2-OB^2}=\sqrt{5^2-3^2}=4\)