
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,mấy đoạn dấu : dấu+ trong đề hơi khó nhìn
\(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(P=\left[\dfrac{\sqrt{x}.\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\left(\dfrac{\sqrt{x}-1+2}{x-1}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{x-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}:\dfrac{1}{\sqrt{x}-1}=\dfrac{x-1}{\sqrt{x}}\)
b, \(P>0=>\dfrac{x-1}{\sqrt{x}}>0=>x-1>0< =>x>1\)(tm)
Vậy \(x>1\) .....
\(\)


=\(\left(3\sqrt{3}-3\sqrt{3}+2\sqrt{6}\right):3\sqrt{3}\)
\(=1-\dfrac{\sqrt{6}}{2}+\dfrac{2\sqrt{2}}{3}\)
=\(\dfrac{6}{6}-\dfrac{3\sqrt{6}}{6}+\dfrac{4\sqrt{2}}{6}\)
=\(\dfrac{6+\sqrt{6}}{6}\)

20.
Đặt \(\left(x;y;z\right)=\left(a^3;b^3;c^3\right)\Rightarrow abc=1\)
\(a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)\ge\left(a+b\right)\left(2ab-ab\right)=ab\left(a+b\right)\)
\(\Rightarrow P=\sum\dfrac{1}{a^3+b^3+1}\le\sum\dfrac{1}{ab\left(a+b\right)+1}=\sum\dfrac{abc}{ab\left(a+b\right)+abc}=\sum\dfrac{c}{a+b+c}=1\)
21.
Đề bài sai, biểu thức này ko tồn tại min hay max (nó chỉ tồn tại khi x;y;z là số thực không âm. Khi đó min P xảy ra tại \(\left(x;y;z\right)=\left(\dfrac{1}{2};\dfrac{1}{2};0\right)\) và hoán vị)
22.
Đề bài sai, biểu thức không tồn tại min. Nó chỉ tồn tại khi có thêm điều kiện x;y;z là độ dài 3 cạnh của 1 tam giác (em cứ thay giá trị \(x=2;y=1.9999;z=8.0001\) vào tính giá trị P sẽ hiểu tại sao đề sai)

2b)
Áp dụng BĐT bunhiacopxki có:
\(\left(1+1\right)\left(x^4+y^4\right)\ge\left(x^2+y^2\right)^2\)
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x+y\right)^2\)\(\Leftrightarrow x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Rightarrow2\left(x^4+y^4\right)\ge\dfrac{\left(x+y\right)^4}{4}\Leftrightarrow x^4+y^4\ge\dfrac{1}{8}.\left(x+y\right)^4\)
Dấu "=" xảy ra khi x=y
3)
Áp dụng bđt Holder có:
\(\left(x^3+y^3+z^3\right)\left(1+1+1\right)\left(1+1+1\right)\ge\left(x+y+z\right)^3\)
\(\Leftrightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\)
Dấu "=" xảy ra khi x=y=z
3)(Nếu không dùng Holder)
Với x,y,z >0, ta có bđt sau:\(2x^3+2y^3+2z^3\ge xy\left(x+y\right)+yz\left(y+z\right)+xz\left(x+z\right)\) (1)
Thật vậy (1)\(\Leftrightarrow\left(x+y\right)\left(x^2-xy+y^2\right)-xy\left(x+y\right)+\left(y+z\right)\left(y^2-yz+z^2\right)-yz\left(y+z\right)+\left(z+x\right)\left(z^2-zx+x^2\right)-zx\left(x+z\right)\ge0\)
\(\Leftrightarrow\left(x+y\right)\left(x-y\right)^2+\left(y+z\right)\left(y-z\right)^2+\left(z+x\right)\left(z-x\right)^2\ge0\) (lđ)
Áp dụng AM-GM có:
\(x^3+y^3+z^3\ge3xyz\)
\(\Leftrightarrow\dfrac{2\left(x^3+y^3+z^3\right)}{3}\ge2xyz\) (2)
Từ (1) và (2), cộng vế với vế \(\Rightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge xy\left(x+y\right)+yz\left(x+z\right)+xz\left(x+z\right)+2xyz\)
\(\Leftrightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge\left(x+y\right)\left(y+z\right)\left(z+x\right)\)
\(\Leftrightarrow8\left(x^3+y^3+z^3\right)\ge3\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
\(\Leftrightarrow9\left(x^3+y^3+z^3\right)\ge x^3+y^3+z^3+3\left(x+y\right)\left(y+z\right)\left(z+x\right)=\left(x+y+z\right)^3\)
\(\Rightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\) (đpcm)

\(3,\\ a,ĐK:x\ge-5\\ PT\Leftrightarrow2\sqrt{x+5}-2\sqrt{x+5}+3\sqrt{x+5}=12\\ \Leftrightarrow\sqrt{x+5}=4\Leftrightarrow x+5=16\Leftrightarrow x=11\left(tm\right)\\ b,ĐK:x\in R\\ PT\Leftrightarrow\left|x-5\right|=6\Leftrightarrow\left[{}\begin{matrix}x-5=6\\5-x=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-1\end{matrix}\right.\)

khi bài toán bắt ta chứng minh một hình gì đó mà thiếu một ta hay một đường thẳng...




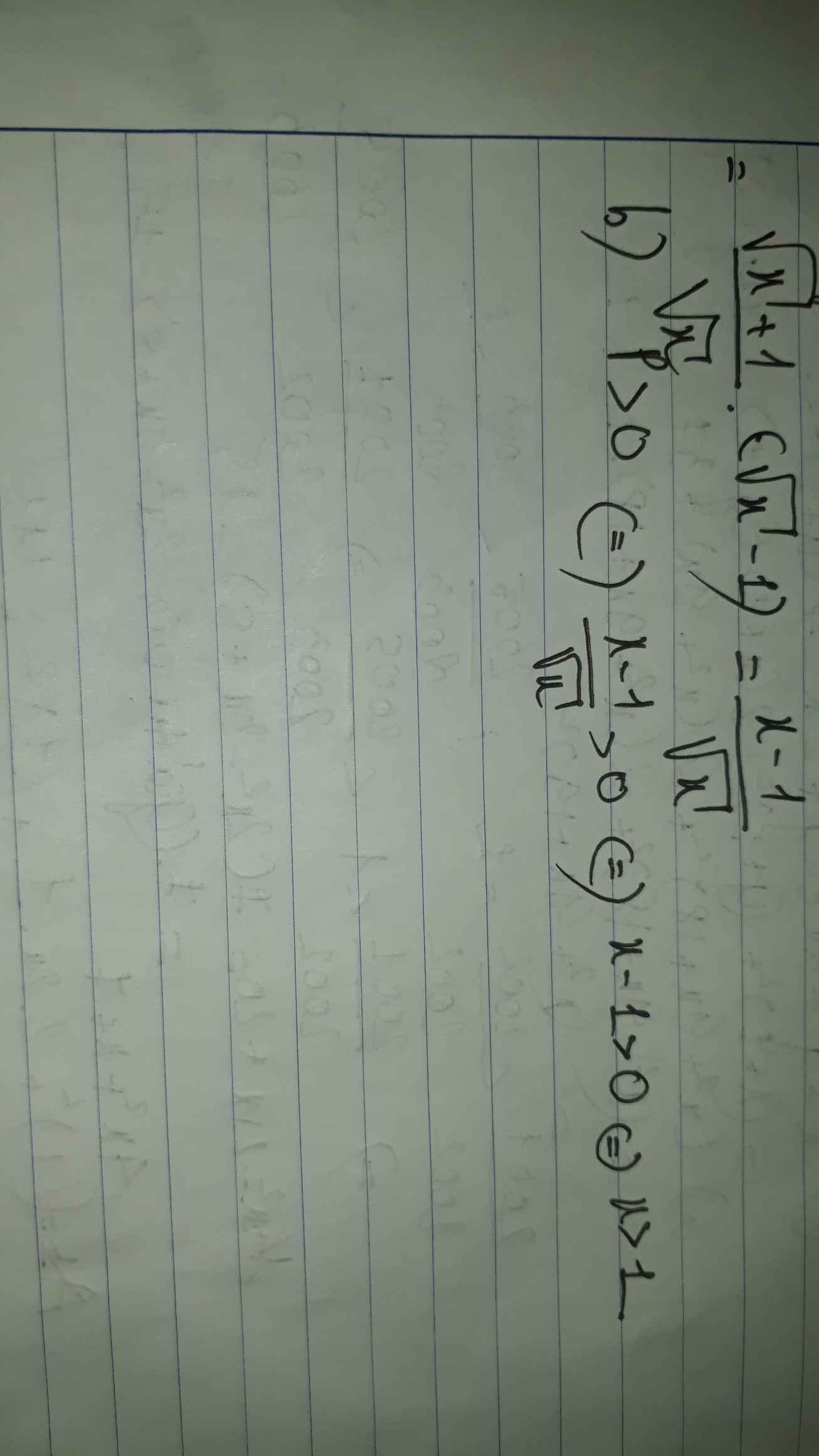



 Giúp mình bài 2b với bài 3 với ạ
Giúp mình bài 2b với bài 3 với ạ


Bài 3:
Phương trình hoành độ giao điểm là:
\(x^2=3x-2\)
=>\(x^2-3x+2=0\)
=>(x-1)(x-2)=0
=>\(\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Khi x=1 thì \(y=1^2=1\)
Khi x=2 thì \(y=2^2=4\)
Vậy: (P) giao (d) tại A(1;1); B(2;4)
bài 2:
a: Thay x=2 vào y=-x+4, ta được:
\(y=-2+2=2=y_A\)
Vậy: A(2;2) thuộc (d)
b: Thay x=2 và y=2 vào y=ax2, ta được:
\(a\cdot2^2=2\)
=>4a=2
=>\(a=\dfrac{1}{2}\)
Khi a=1/2 thì (P): \(y=\dfrac{1}{2}x^2\)
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=-x+4\)
=>\(\dfrac{1}{2}x^2+x-4=0\)
=>\(x^2+2x-8=0\)
=>(x+4)(x-2)=0
=>\(\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)
Khi x=-4 thì \(y=-\left(-4\right)+4=8\)
Vậy: Giao điểm thứ hai là B(-4;8)
c: O(0;0); A(2;2); B(-4;8)
\(OA=\sqrt{\left(2-0\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(OB=\sqrt{\left(-4-0\right)^2+\left(8-0\right)^2}=4\sqrt{5}\)
\(AB=\sqrt{\left(-4-2\right)^2+\left(8-2\right)^2}=6\sqrt{2}\)
Vì \(OA^2+AB^2=OB^2\)
nên ΔAOB vuông tại A
=>\(S_{AOB}=\dfrac{1}{2}\cdot AB\cdot AO=\dfrac{1}{2}\cdot2\sqrt{2}\cdot6\sqrt{2}=12\)