Ta có:

A-B=2m^3+3m^3-4mn^2

TH1

Nếu m > n. Đặt m=n+x

óA-B=2(n+x)^3+3m^3-4(n+x)n^2

óA-B=2(n^3+3n^2x+2nx^2+x^3)=3m^3-4n^3-4n^2x

óA-B=n^3+2n^2x+6nx^2+2x^3>0

Vậy A>B

TH2                     

Nếu m < n. Đặt n=m+y

óA-B=2m^3+3(m+y)^3-4m(m+y)^2

óA-B=2m^3+3(m^3+3m^2y+3my^2+y^3)-4m^3-8m^2y-4my^2

óA-B=m^3+m^2y+5my^2+3y^3> 0

Vậy A > B

a) Thay m = -1 và n = 2 ta có:

3m - 2n = 3(-1) -2.2 = -3 - 4 = -7

b) Thay m = -1 và n = 2 ta được 

7m + 2n - 6 = 7.(-1) + 2.2 - 6 = -7 + 4 - 6 = -9.

Xét trường hợp thoy:))

Xét \(m>n\).Đặt \(m=n+k\) với \(k\in N\)

Xét \(A-B=2m^3+3n^3-4mn^2\)

\(A-B=2\left(n+k\right)^3+3n^3-4\left(n+k\right)n^2\)

\(A-B=2n^3+6n^2k+6nk^2+2k^3+3n^3-4n^3-4n^2k\)

\(A-B=n^3+2n^2k+6nk^2+2k^3>0\)

Xét \(m< n\).Đặt \(n=m+k\)

Ta có:

\(A-B=2m^3+3n^3-4mn^2\)

\(A-B=2m^3+3\left(m+k\right)^3-4m\left(m+k\right)^2\)

\(A-B=2m^3+3m^3+9m^2k+9mk^2+3k^3-4m^3-8m^2k-4mk^2\)

\(A-B=m^3+m^2k+5mk^2+3k^2>0\)

Xét \(m=n\)

Ta có:

\(A=2m^3+3n^3=2m^3+3m^3=5m^3\)

\(B=4mn^2=4mm^2=4m^3\)

\(\Rightarrow A>B\)

Vậy \(A>B\) 

b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)

\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)

\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)

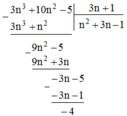
Ta có:  3 n 3 + 10 n 2 - 5  = 3 n + 1 n 2 + 3 n - 1 - 4

Để phép chia đó là chia hết thì 4 ⋮ 3n + 1⇒ 3n + 1 ∈ Ư(4)

       3n + 1 ∈ {-4; -2; -1; 1; 2; 4}

       3n + 1 = -4⇒ 3n = -5⇒ n = 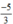 ∉ Z : loại

       3n + 1 = -2⇒ 3n = -3⇒ n = -1 ∈ Z

       3n + 1 = -1⇒ 3n = -2⇒ n = 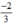 ∉ Z : loại

       3n + 1 = 1⇒ 3n = 0⇒ n = 0 ∈ Z

       3n + 1 = 2⇒ 3n = 2⇒ n = 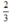 ∉ Z : loại

       3n + 1 = 4⇒ 3n = 3⇒ n = 1 ∈ Z

Vậy n ∈ {-1; 0; 1} thì  3 n 3 + 10 n 2 - 5  chia hết cho 3n + 1.

Cho m là số nguyên nhỏ hơn 30. Có bao nhiêu giá trị của m để đa thức x² + mx + 72 là tích của 2 đa thức bậc nhất là số nguyên với hệ số là số nguyên. 
--------------------------------------... 
Gọi 2 đa thức bậc nhất đó là ax+b và cx+d với a, b, c, d nguyên 

Ta có: (ax+b)(cx+d) = acx² + (ad + bc)x + bd (1) 

a = c = ±1 , (1) trở thành: x² + ±(b+d)x + bd 

Đồng nhất 1 với đa thức đề cho, ta có: bd = 72 và ±(b+d) = m 

Các ước nguyên của 72 là : ± 1, ± 2 , ± 3, ± 4, ±6, ±8, ±9, ±12, ±18, ±24 , ±36, ± 72 

Các bộ số (b,d) là (±1,±72) , (±2,±36) , (±3, ±24) , (±4,±18) , (±6, ±12) , (±8,±9) bạn nhớ là b và d cùng dấu nhé vì tích của chúng >0 

Từ đây có thể tìm thấy có 10 số nguyên m nhỏ hơn 30 thỏa m = ±(b+d) với bd = 72 là: -73, -38, ±27 , ±22 , ±18 , ±17 

Nếu bài hỏi số nguyên dương thì chỉ có 4 số thôi : 17, 18, 22, 27 

k mk nhá!!!ố~ồ

Đáp án này trên yahoo nha 

 Cho m là số nguyên nhỏ hơn 30. Có bao nhiêu giá trị của m để đa thức x^2 + mx + 72 là tích của 2 đa thức bậc nhất là số nguyên với hệ số là số nguyên.
--------------------------------------... 
Gọi 2 đa thức bậc nhất đó là ax+b và cx+d với a, b, c, d nguyên 

Ta có: (ax+b)(cx+d) = acx^2 + (ad + bc)x + bd (1) 

a = c = ±1 , (1) trở thành: x^2 + ±(b+d)x + bd 

Đồng nhất 1 với đa thức đề cho, ta có: bd = 72 và ±(b+d) = m 

Các ước nguyên của 72 là : ± 1, ± 2 , ± 3, ± 4, ±6, ±8, ±9, ±12, ±18, ±24 , ±36, ± 72 

Các bộ số (b,d) là (±1,±72) , (±2,±36) , (±3, ±24) , (±4,±18) , (±6, ±12) , (±8,±9) bạn nhớ là b và d cùng dấu nhé vì tích của chúng >0 

Từ đây có thể tìm thấy có 10 số nguyên m nhỏ hơn 30 thỏa m = ±(b+d) với bd = 72 là: -73, -38, ±27 , ±22 , ±18 , ±17 

Nếu bài hỏi số nguyên dương thì chỉ có 4 số thôi : 17, 18, 22, 27 
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~...

Tích nha