Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đầu bài ta có :
\(\begin{cases}u_2-u_1=7\\u_3-u_2=14\\u_4-u_3=21.......\\....u_n-u_{n-1}=7\left(n-1\right)\end{cases}\)
Cộng các vế của các phương trình của hệ, ta được :
\(\Leftrightarrow u_n-u_1=7+14+21+.....+7\left(n-1\right)=7\frac{n\left(n-1\right)}{2}\left(1\right)\)
Đặt \(u_n=35351\Rightarrow\left(1\right)\Leftrightarrow35351-1=7\frac{n\left(n-1\right)}{2}\)
\(\Leftrightarrow n^2-n-10100=0\rightarrow n=101\)
Do đó 35351 là số hạng thứ 101 của dãy số

Câu 1:
Dãy đã cho có thể viết dưới dạng công thức truy hồi sau:
\(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=u_n+7n\end{matrix}\right.\)
\(u_{n+1}=u_n+7n\Leftrightarrow u_{n+1}-\dfrac{7}{2}\left(n+1\right)^2+\dfrac{7}{2}\left(n+1\right)=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\)
Đặt \(v_n=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\Rightarrow\left\{{}\begin{matrix}v_1=1\\v_{n+1}=v_n\end{matrix}\right.\)
\(\Rightarrow v_{n+1}=v_n=v_{n-1}=...=v_1=1\)
\(\Rightarrow u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n=1\)
\(\Leftrightarrow u_n=\dfrac{7}{2}n^2-\dfrac{7}{2}n+1\)
\(\dfrac{7}{2}n^2-\dfrac{7}{2}n+1=35351\)
\(\Leftrightarrow\dfrac{7}{2}n^2-\dfrac{7}{2}n-35350=0\)
\(\Rightarrow n=101\)
Vậy đó là số hạng thứ 101
2.
Do a;b;c lập thành 1 cấp số cộng
\(\Rightarrow a+c=2b\)
\(\Leftrightarrow2R.sinA+2R.sinC=2.2R.sinB\)
\(\Leftrightarrow sinA+sinC=2sinB\)
\(\Leftrightarrow2sin\dfrac{A+C}{2}.cos\dfrac{A-C}{2}=4sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{B}{2}cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}=2cos\dfrac{A+C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)+sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)=2cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)-2sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right).cos\left(\dfrac{C}{2}\right)=3sin\left(\dfrac{A}{2}\right).sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cot\left(\dfrac{A}{2}\right).cot\left(\dfrac{C}{2}\right)=3\)

Gọi ba số đó là \(x,y,z\). Do ba số là các số hạng thứ hai, thứ 9 và thứ 44 của một cấp số cộng nên:
\(x;y=x+7d;z=x+42d\). (Với d là công sai của cấp số cộng).
Ta có: \(x+y+z=x+x+7d+x+42d=3x+49d=217\).
Mặt khác x, y, z là các số hạng liên tiếp của một cấp số nhân nên:
\(y^2=xz\)\(\Leftrightarrow\left(x+7d\right)^2=x\left(x+42d\right)\)\(\Leftrightarrow-28xd+49d^2=0\)\(\Leftrightarrow7d\left(-4x+7d\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}d=0\\-4x+7d=0\end{matrix}\right.\).
Với \(d=0\) suy ra \(x=y=z=\dfrac{217}{3}\).
Suy ra: \(n=820:\dfrac{217}{3}=\dfrac{2460}{217}\notin N\).
Với \(4+7d=0\). Ta có hệ:
\(\left\{{}\begin{matrix}4x+7d=0\\3x+49d=217\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=7\\d=4\end{matrix}\right.\).
Vậy \(u_1=7-4=3\).
Có \(S_n=\dfrac{\left[2u_1+\left(n-1\right)d\right]n}{2}=\dfrac{\left[2.3+\left(n-1\right)4\right]n}{2}=820\)
\(\Rightarrow n=20\left(tm\right)\).
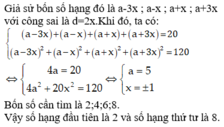

Chọn C
Theo đề bài ta có:
Cộng vế với vế các phương trình của hệ ta được: