Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)
a)Ảnh của một vật tạo bởi gương phẳng có đặc điểm:
- Là ảnh ảo (không hứng được trên màn chắn).
- Có kích thước lớn bằng vật.
- Đối xứng với vật qua gương phẳng (tức là khoảng cách từ một điểm của vật đến gương phẳng bằng khoảng cách từ ảnh của điểm đó đến gương)
* Muốn vẽ ảnh của một vật tạo bởi gương phẳng ta vẽ ảnh của các điểm đặc biệt trên ảnh sau đó nối các điểm ảnh cho ta ảnh của vật.
* Muốn vẽ ảnh của một điểm ta dựa vào:
- Định luật phản xạ ánh sáng.
Vẽ thì tự vẽ mk ko bt vẽ vật
B)Tia RI=AI vì tia tới = tia phản xạ
a)Ảnh của một vật tạo bởi gương phẳng có đặc điểm:
- Là ảnh ảo (không hứng được trên màn chắn).
- Có kích thước lớn bằng vật.
- Đối xứng với vật qua gương phẳng (tức là khoảng cách từ một điểm của vật đến gương phẳng bằng khoảng cách từ ảnh của điểm đó đến gương)
* Muốn vẽ ảnh của một vật tạo bởi gương phẳng ta vẽ ảnh của các điểm đặc biệt trên ảnh sau đó nối các điểm ảnh cho ta ảnh của vật.
* Muốn vẽ ảnh của một điểm ta dựa vào:
- Định luật phản xạ ánh sáng.
Vẽ thì tự vẽ mk ko bt vẽ vật
B)Tia RI=AI vì tia tới = tia phản xạ

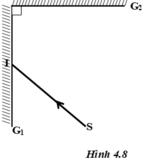
a, Đầu tiên vẽ tia tới chiếu đến gương G1 tại I, rồi phản đến gương G2 tại điểm I' , rồi phản xạ tiếp qua điểm R
b, Ta có tia pháp tuyến \(NI\perp I\) (G1) , \(NI'\perp I'\left(G2\right)\)
mà 2 gương G1 , G2 vuông góc vói nhau
\(\Rightarrow\left\{{}\begin{matrix}i=90^o-45^o=45^o\\i=i'\Leftrightarrow i'=45^o\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}i2=90^o-45^o=45^o\\i2=i2'\Leftrightarrow i2'=45^o\end{matrix}\right.\)
Góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên gương G2 : \(45^o+45^o+45^o+45^o=180^o\)
Tham khảo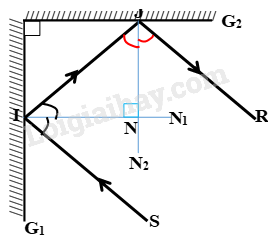
Do hai gương đặt vuông góc với nhau nên hai pháp tuyến IN1IN1 và JN2JN2 cũng vuông góc với nhau.
Định luật phản xạ tại gương G1G1:
ˆSIN=ˆNIJ⇒ˆSIJ=2ˆNIJ(1)SIN^=NIJ^⇒SIJ^=2NIJ^(1)
Định luật phản xạ tại gương G2G2:
ˆIJN=ˆNJR⇒ˆIJR=2ˆIJN(2)IJN^=NJR^⇒IJR^=2IJN^(2)
ΔIJNΔIJN vuông tại NN:
ˆNIJ+ˆNJI=900NIJ^+NJI^=900
⇒ˆSIJ+ˆIJR=2ˆNIJ+2ˆNJI=2(ˆNIJ+ˆNJI)=1800⇒SIJ^+IJR^=2NIJ^+2NJI^=2(NIJ^+NJI^)=1800
Vậy tia tới SISI song song với tia phản xạ JRJR. Góc tạo bởi tia tới SISI và tia phản xạ cuối cùng trên gương G2G2 có giá trị 1800

Đáp án: A.
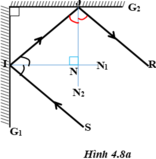
Do hai gương đặt vuông góc với nhau nên hai pháp tuyến IN1 và JN2 cũng vuông góc với nhau.
Định luật phản xạ tại gương G1:
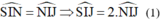
Định luật phản xạ tại gương G2:
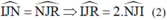
Tam giác IJN vuông tại N:
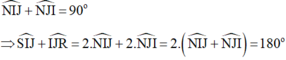
→ Tia tới SI song song với tia phản xạ JR. Góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên gương G2 có giá trị 180o

Giả sử tia tới là SI có góc tới là: \(i=\widehat{SIN}=a\)
Định luật phản xạ tại gương \(G_1:\) \(\widehat{SIN}=\widehat{NIR}=a\left(1\right)\)
Do hai gương đặt song song với nhau nên pháp tuyến IN ở gương \(G_1\) và pháp tuyến \(RN'\) ở gương \(G_2\) song song với nhau, tia phản xạ ở \(G_1\) chính là tia tới ở gương \(G_2\) : \(\widehat{N'RI}=\widehat{RIN}=a\)
Định luật phản xạ tại gương \(G_2\) : \(\widehat{IRN}'=\widehat{N'RK}=a\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ta có: \(\widehat{SIR}=\widehat{IRK}=2a\)
Vì hai góc này so le trong nên SI // RK. Nên góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên gương \(G_2\) có giá trị \(0^o\)
\(\Rightarrow ChọnA\)