

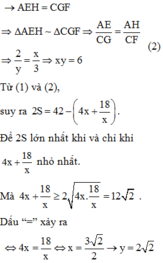
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


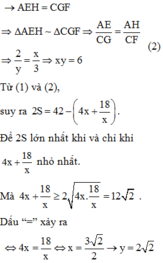

Đáp án C
Ta có S E F G H nhỏ nhất ⇔ S = S Δ A E H + S Δ C G F + S Δ D G H lớn nhất (do S Δ B E F không đổi)
⇒ 2 S = 2 x + 3 y + 6 − x 6 − y = x y − 4 x − 3 y + 36 1
Ta có E F G H là hình thang
⇒ A E H ⏜ = C G F ⏜ ⇒ Δ A E H ∽ Δ C G F
⇒ A E C G = A H C F ⇔ 2 y = x 3 ⇒ x y = 6 2
Từ (1), (2) ⇒ 2 S = 42 − 4 x + 18 x
Để 2S lớn nhất thì 4 x + 18 x nhỏ nhất
Mà 4 x + 18 x ≥ 12 2 . Dấu “=” khi
4 x + 18 x ⇔ x = 3 2 2 ⇒ y = 2 2 ⇒ x + y = 7 2 2

Đáp án C
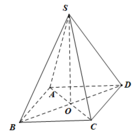
S A = 1 − x 2 2 2 + 1 4 = 1 − x 2 + x 2 2 A O = x 2 2 , S O = S A 2 − A O 2 = 1 − x 2 + x 2 − x 2 2 = 1 − x 2 2 V = 1 3 S O . S A B C D = 1 3 x 2 1 − x 2 2 f ( x ) = x 2 1 − x 2 2 , x ∈ 0 ; 1 f ' ( x ) = 4 x − 5 2 x 2 4 1 − x 2 2 f ' ( x ) = 0 ⇔ x = 0 ( L ) x = 2 2 5

Đáp án D
Hàm số f(x) có dạng f ( x ) = ( x + 2 ) ( x - 1 ) 2 Giao với trục Oy tại (0, 2) .
=> 2<m<4.
Chọn phương án D.