a: Xet ΔOAC có OA=OC và OA^2+OC^2=AC^2

nên ΔOAC vuôg cân tại O

b: \(BC=\sqrt{AB^2-AC^2}=\sqrt{4R^2-2R^2}=R\sqrt{2}\)

c: ΔOAC vuông cân tại O

=>góc BAC=45 độ

Bài 2: Cho nửa đường tròn (O) đường kính AB, điểm C thuộc nửa đường tròn có số đo bằng 60o. Gọi E, F lần lượt là điểm chính giữa của các cung AC và BC, I là giao điểm của AF và BE

a) Tính số đo các góc của .

b) Chứng minh: CI là phân giác của góc ACB

c) Chứng minh: Tứ giác ABFC là hình thang cân.

C thuộc nửa đường tròn có số đo bằng 60^o tức là \(\widehat{AOC}\) hay \(\widehat{BOC}\) bằng 60^o vậy bạn?

a: góc EAB=1/2*90=45 độ

=>góc AEB=45 độ

b: góc EFD=góc FAB+góc FBA=90 độ+góc DAB

góc ECD+góc ACD=180 độ

=>góc ECD=góc DBA

=>góc EFD+góc ECD=180 độ

=>CDFE nội tiếp

a) Ta có \(\widehat{BOM}=sđ\stackrel\frown{BM}\) (đ/lí góc ở tâm)
Mà \(\stackrel\frown{BM}=120^o=>\widehat{BOM}=120^o\)
Vì \(\widehat{BOM}+\widehat{AOM}=180^o=>\widehat{AOM}=60^o\)
Xét \(\Delta AOM\) có 
OA = OM (bán kính)
\(\widehat{AOM}=60^o\left(cmt\right)\)
\(=>\Delta OAM\) đều (dhnb tam giác đều)
b) +) Ta có \(\widehat{AMB}=90^o\) (góc nội tiếp chắn nửa đường tròn)
mà \(\Delta OAM\) đều (cmt) \(=>\widehat{OAM}=60^o\)
\(=>\widehat{ABM}=30^o\)
+) Vì R = 3 cm (gt) => OA = OB = 3 cm => AB = 6cm 
Xét \(\Delta AMB\) vg tại A 
\(=>AB^2=AM^2+BM^2\)
\(=>6^2=3^2+BM^2\)
\(=>BM=3\sqrt{3}\)

a: Xét (O) có

ΔBAC nội tiếp

AC là đường kính

Do đó: ΔBAC vuông tại B

Xét (O) có

\(\widehat{BAC}\) là góc nội tiếp chắn cung BC

Do đó: \(\widehat{BAC}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BC}=\dfrac{1}{2}\cdot60^0=30^0\)

Gọi H là giao điểm của BD với AC

BD\(\perp\)AC nên BD\(\perp\)AC tại H

ΔOBD cân tại O

mà OH là đường cao

nên H là trung điểm của BD

Xét ΔCBD có

CH là đường cao

CH là đường trung tuyến

Do đó: ΔCBD cân tại C

=>CB=CD

Xét ΔCOD và ΔCOB có

CD=CB

OD=OB

CO chung

Do đó: ΔCOD=ΔCOB

=>\(\widehat{COD}=\widehat{COB}\)

=>\(sđ\stackrel\frown{CB}=sđ\stackrel\frown{CD}=60^0\)

Xét ΔBAC vuông tại B có \(\widehat{BAC}+\widehat{BCA}=90^0\)

=>\(\widehat{BCA}+30^0=90^0\)

=>\(\widehat{BCA}=60^0\)

Xét (O) có

\(\widehat{BCA}\) là góc nội tiếp chắn cung AB

Do đó: \(\widehat{BCA}=\dfrac{1}{2}\cdot sđ\stackrel\frown{AB}\)

=>\(sđ\stackrel\frown{AB}=2\cdot\widehat{BCA}=120^0\)

DF//AC

DB\(\perp\)AC

Do đó: DF\(\perp\)DB

=>ΔDFB vuông tại D

ΔDFB vuông tại D

nên ΔDFB nội tiếp đường tròn đường kính BF

mà ΔDFB nội tiếp (O)

nên O là trung điểm của BF

=>OA//DF

=>\(\widehat{BFD}=\widehat{BOH}=\widehat{BOC}\)(hai góc đồng vị)

=>\(\widehat{BFD}=60^0\)

ΔBDF vuông tại D

=>\(\widehat{BFD}+\widehat{FBD}=90^0\)

=>\(\widehat{FBD}+60^0=90^0\)

=>\(\widehat{FBD}=30^0\)

Xét (O) có

\(\widehat{FBD}\) là góc nội tiếp chắn cung FD

Do đó: \(\widehat{FBD}=\dfrac{1}{2}\cdot sđ\stackrel\frown{FD}\)

=>\(sđ\stackrel\frown{FD}=2\cdot\widehat{FBD}=2\cdot\)30=60 độ

giải b1 , hình ảnh tham khảo:

giải b2:

a, MPHQ là hình chữ nhật => MH = PQ

b, Sử dụng hệ thức lượng trong tam giác vuông chứng minh được MP.MA = MQ.MB => ∆MPQ: ∆MBA

c,\(\widehat{PMH}=\widehat{MBH}\Rightarrow\widehat{PQH}=\widehat{O_2QP}\)  => PQ là tiếp tuyến của \(\left(O_2\right)\) 

Tương tự PQ cũng là tiếp tuyến \(\left(O_1\right)\)

hình( tự vẽ)

a) Chú ý: \(\widehat{AEB}=\widehat{AFB}=90\)(góc chắn nửa đường tròn) => H là trực tâm tam giác ABC

=> tứ giác AIFC nội tiếp (do \(\widehat{AIC}=\widehat{AFC}=90\)) => góc CIF= góc CAF

mà góc CAF=\(\frac{1}{2}\)góc EOF

mà EF=R => tam giác OEF đều => EOF =60 => CIF=30

b)

tam giác vuông AIC đồng dạng với tam giác vuông AEB (g-g)

=> AE.AC=AI.AB

Tương tự tam giác BIC đồng dạng BFA

=> BF.BC=BI.AB

Vậy: AE.AC+BF.BC=AB(AI+IB)=AB\(^2\)=4R\(^2\)=const (ĐPCM)

Sorry , mk ms học lớp 6 ... 
Have a nice day !!!

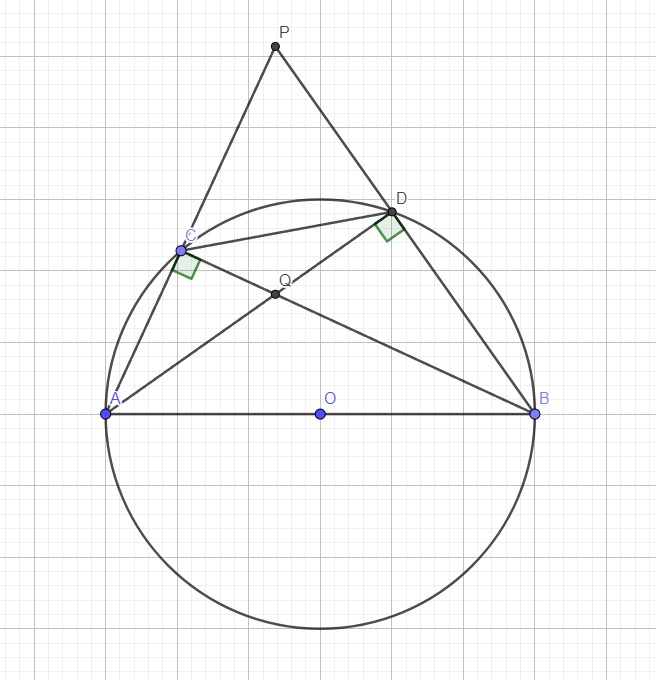
Do \(OC=OD=CD=R\Rightarrow\Delta OCD\) là tam giác đều

\(\Rightarrow\widehat{COD}=60^0\)

Mà \(\widehat{CAD}=\dfrac{1}{2}\widehat{COD}\) (góc nt và góc ở tâm cùng chắn CD)

\(\Rightarrow\widehat{CAD}=30^0\)

AB là đường kính nên \(\widehat{ADB}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ADB}=90^0\)

\(\Rightarrow\widehat{ADP}=90^0\Rightarrow\widehat{APB}=180^0-\left(90^0+30^0\right)=60^0\)

Tương tự ta có \(\widehat{ACB}\) là góc nt chắn nửa đường tròn

\(\Rightarrow\widehat{ACB}=90^0\Rightarrow\widehat{BCP}=90^0\)

\(\Rightarrow\widehat{CQD}=360^0-\left(\widehat{APB}+\widehat{ADP}+\widehat{ACB}\right)=360^0-\left(60^0+90^0+90^0\right)=120^0\)

\(\Rightarrow\widehat{AQB}=\widehat{CQD}=120^0\) (2 góc đối đỉnh)