Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét △AKC và △DBC có: C = 900, góc KAC = góc CDB (cùng phụ với góc B) => △AKC đồng dạng với △DBC => AC/DC = KC/BC=> KC.DC = AC.BC (✳)
Cũng có △IAB vuông tại I có IC vuông góc với AB nên theo hệ thức lượng trong tam giác vuông ta có IC2=AC.CB (**)
Từ (*) và (**) => KC.DC=IC2 => KC/IC=IC/DC=1/2 => DC = 2IC
IC2=AC.BC=1/2R . 3/2R = 3/4R2 =>IC = \(\sqrt{ }\)3/2 R=> DC = căn 3 R.
S△ADB = 1/2 DC.AB=căn 3 R2

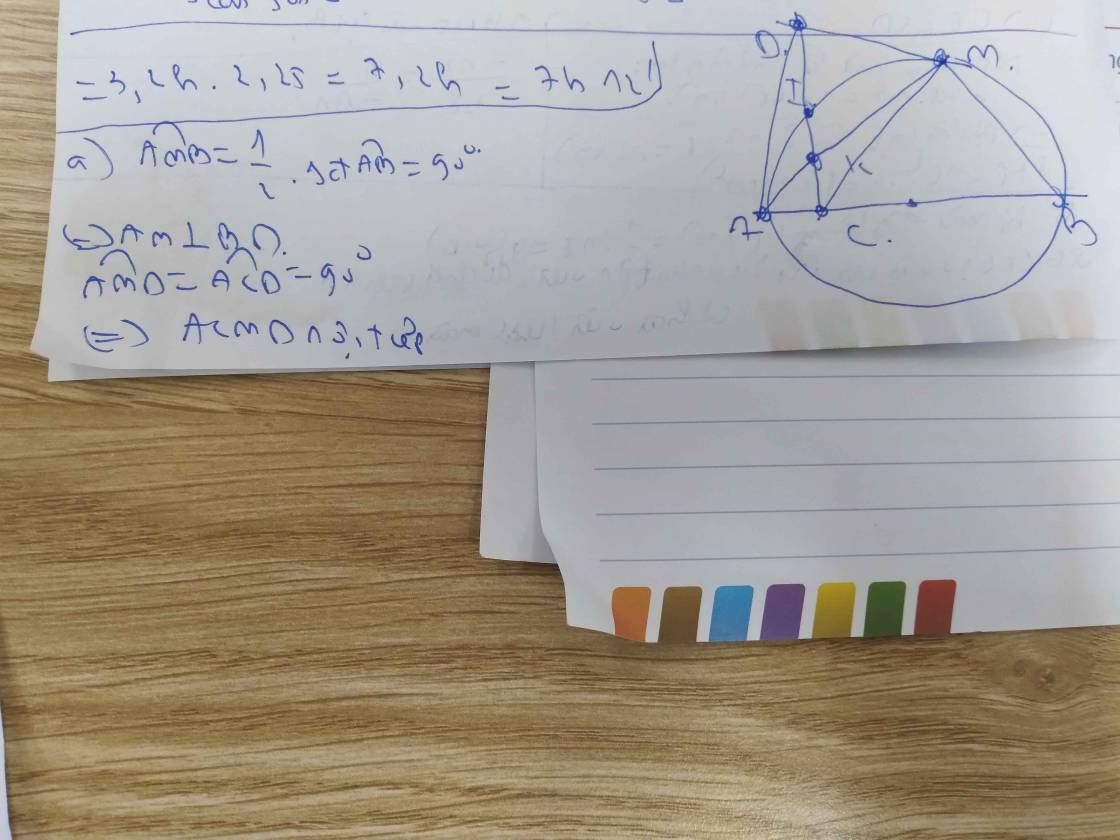
a) Vì AB là đường kính \(\Rightarrow\angle AMB=90\Rightarrow\angle ACD=\angle AMD=90\)
\(\Rightarrow ACMD\) nội tiếp
b) Ta có: \(\angle KCB+\angle KMB=90+90=180\Rightarrow KCBM\) nội tiếp
\(\Rightarrow\angle AKC=\angle MBA\)
Ta có: \(\angle NMK=\angle MBA=\angle AKC=\angle MKN\)
\(\Rightarrow\Delta NMK\) cân tại N
c) Vì B và E đối xứng với nhau qua C \(\Rightarrow\) CD là trung trực BE
\(\Rightarrow\angle DEC=\angle DBC=\angle AKC\Rightarrow AKDE\) nội tiếp

1:
góc AMB=1/2*sđ cung AB=90 độ
=>AM vuông góc BD
góc ACD=góc AMD=90 độ
=>ACMD nội tiếp
góc KCB+góc KMB=180 độ
=>BMKC nội tiếp
2: Xét ΔCAK vuông tại C và ΔCDB vuông tại C có
góc CAK=góc CDB
=>ΔCAK đồng dạng với ΔCDB
=>CA/CD=CK/CB
=>CA*CB=CD*CK

a) Xét (O) có
ΔAMB nội tiếp đường tròn(A,M,B\(\in\)(O))
AB là đường kính(gt)
Do đó: ΔMAB vuông tại M(Định lí)
\(\Leftrightarrow AM\perp MB\) tại M
\(\Leftrightarrow AM\perp BD\) tại M
\(\Leftrightarrow\widehat{AMD}=90^0\)
Xét tứ giác ADMC có
\(\widehat{AMD}=\widehat{ACD}\left(=90^0\right)\)
\(\widehat{AMD}\) và \(\widehat{ACD}\) là hai góc cùng nhìn cạnh AD
Do đó: ADMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
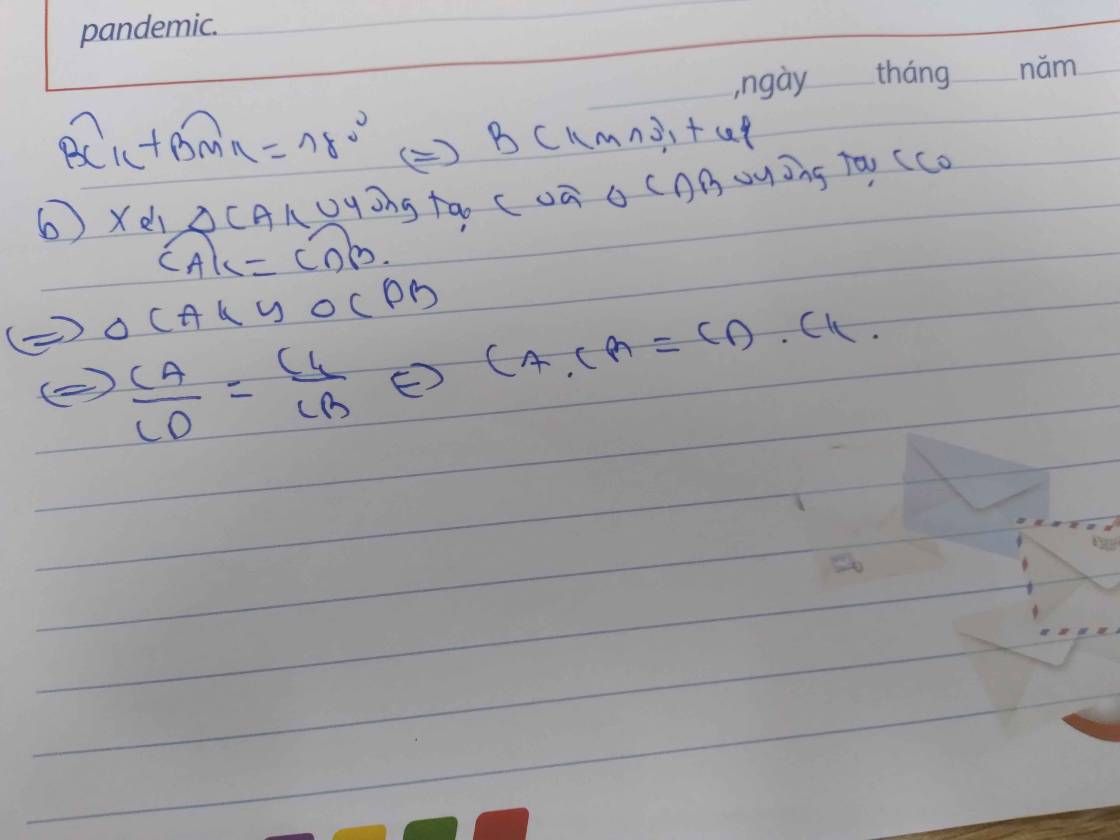



Ơ , em tưởng chị " ko cần bít " cơ mà ?