Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
MC là tiếp tuyến
MA là tiếp tuyến
Do đó: MC=MA
Xét (O) có
NB là tiếp tuyến
NC là tiếp tuyến
Do đó: NB=NC
Ta có: MN=MC+CN
nên MN=MA+NB

Vì M,N là giao 2 tiếp tuyến nên \(AM=MC;BN=ND\)
Lại có \(OA=OB=OC=R\) nên OM,ON lần lượt là trung trực của tam giác OAC và OBC cân tại O
Do đó OM,ON cũng là phân giác của \(\widehat{AOC};\widehat{COB}\)
Vậy \(\widehat{MON}=\widehat{MOC}+\widehat{CON}=\dfrac{1}{2}\left(\widehat{AOC}+\widehat{COB}\right)=90^0\) (kề bù)

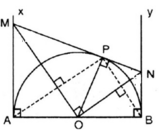
a) Ta có OM, ON lần lượt là tia phân giác của AOP, BOP (tính chất của hai tiếp tuyến cắt nhau).
Mà AOP kề bù với BOP nên suy ra OM vuông góc với ON.
Vậy ΔMON vuông tại O.
Góc  là góc nội tiếp chắn nửa đường tròn nên
là góc nội tiếp chắn nửa đường tròn nên  = 900
= 900
Tứ giác AOPM có:
![]()
Suy ra, tứ giác AOPM nội tiếp đường tròn.
![]()
Xét ∆ MON và ∆ APB có:
![]()
=> Hai tam giác MON và APB đồng dạng
b)
* Tam giác MON vuông tại O có đường cao OP nên
OP2 = MP. NP (1)
* Theo tính chất hai tiếp tuyến cắt nhau ta có
MA= MP và NB = NP (2)
Từ (1) và (2) suy ra: OP2 = MA. NB hay R2 = MA. NB ( đpcm)
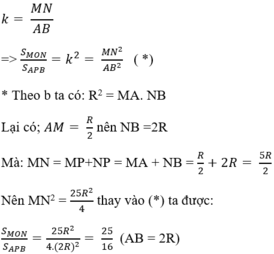
c) * Theo a, ∆MON và APB đồng dạng với nhau với tỉ số đồng dạng là:
d) Nửa hình tròn APB quay quanh AB tạo ta hình cầu có bán kính R.
nên thể tích khối cầu tạo ra là: 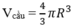

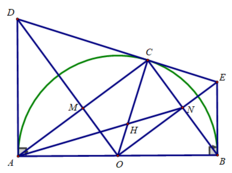
a) CE và EB là 2 tiếp tuyến cắt nhau tại E
⇒ EC = EB và CB ⊥ OE
Tương tự, DC và DA là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DA và AC ⊥ OD
Khi đó: AD + BE = DC + EC = DE

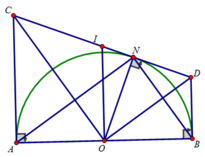
b) Gọi I là tâm của đường tròn đường kính CD.
Tứ giác CABD là hình thang vuông (AC ⊥ AB;BD ⊥ AB) có OI là đường trung bình
⇒ OI // AC ; mà AC ⊥ AB ⇒ OI ⊥ AB tại O
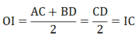
Vậy AB tiếp xúc với đường tròn đường kính CD.
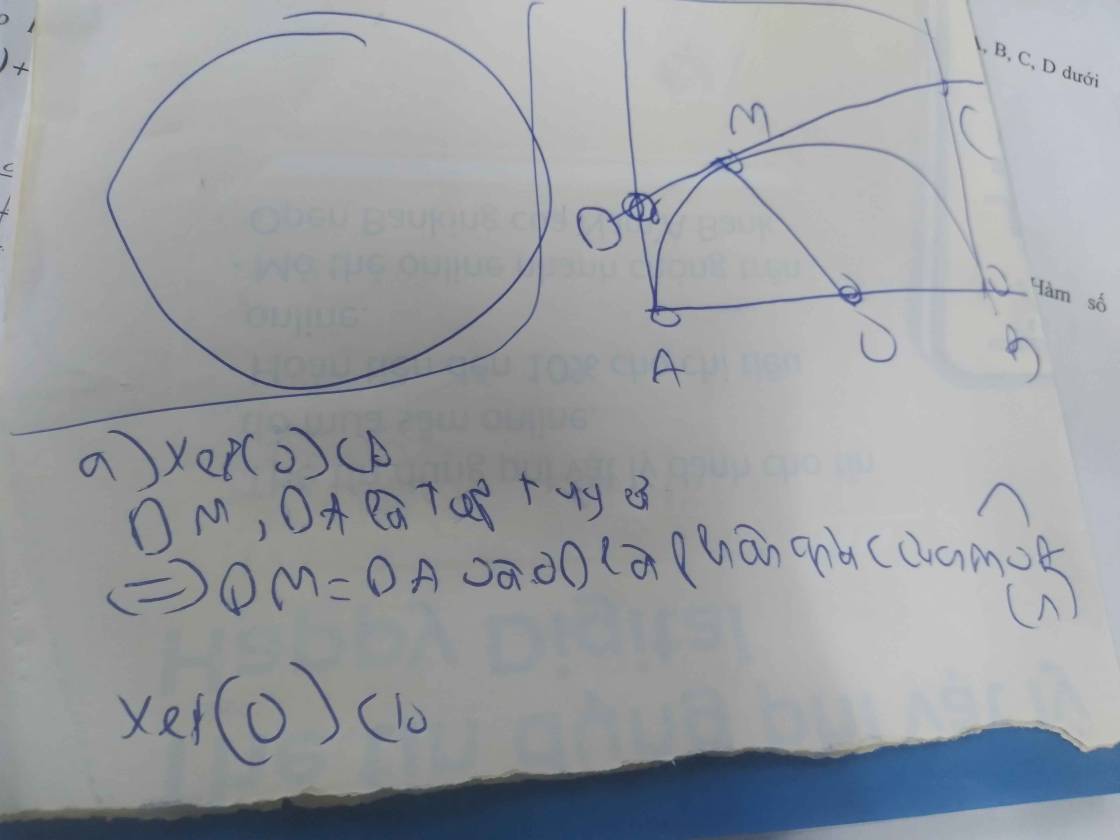

a: Xét (O) có
MA là tiếp tuyến
MC là tiếp tuyến
Do đó: MA=MC
Xét (O) có
NC là tiếp tuyến
NB là tiếp tuyến
Do đó: NC=NB
Ta có: CM+CN=MN
nên MN=MA+NB