Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tứ giác BCEF có
\(\widehat{BEC}=\widehat{CFB}\left(=90^0\right)\)
\(\widehat{BEC}\) và \(\widehat{CFB}\) là hai góc cùng nhìn cạnh BC
Do đó: BCEF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

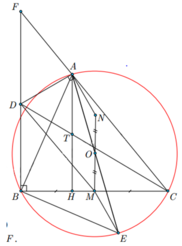
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .

a) Vì tứ giác BFEC nội tiếp nên \(\widehat{PFB}=\widehat{ACB}=\widehat{PBF}\) suy ra \(PF=PB\)
Suy ra \(MP\perp AB\) vì MP là trung trực của BF. Do đó \(MP||CF\). Tương tự \(MQ||BE\)
b) Dễ thấy M,I,J đều nằm trên trung trực của EF cho nên chúng thẳng hàng. Vậy IJ luôn đi qua M cố định.
c) Gọi FK cắt AD tại T ta có \(FK\perp AD\) tại T. Theo hệ thức lượng \(IE^2=IF^2=IT.IL\)
Suy ra \(\Delta TIE~\Delta EIL\). Lại dễ có \(EI\perp EM\), suy ra ITKE nội tiếp
Do vậy \(\widehat{ILE}=\widehat{IET}=\widehat{IKT}=90^0-\widehat{LIK}\). Vậy \(IK\perp EL.\)