Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

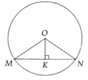
a, Tính được OK = R 2
b, Tính được
M
O
K
^
=
60
0
;
M
O
N
^
=
120
0
c, HS tự làm

a) Xét ΔOAB có OA=OB=AB(=R)
nên ΔOAB đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{AOB}=60^0\)
\(\Leftrightarrow sđ\stackrel\frown{AB}=60^0\)

cau a, thi de roi
có góc FKE a góc nội tiếp chắn nửa đt(O)=>goc FKE=90
tam giác FHS đồng dạng với tam giác PKS vi:
FSH=PSK
EFK=EPH(vì E là điểm chính giữa cung lớn MN=>cũng EN=cũng MEFK là góc nội tiếp EHP là góc có đỉnh ngoài đt(O))(ban tu tinh 2 goc do )
nen PHF=PKF=90=>PHE=90 =>TU GIAC NT(2 GOC DOI 180)
DT(O) CO EH vuong goc voiMN (PHE=90) nen EH la duong trung truc cua MN=>FN=FM=>cung FN=cungFM(may cai nay co trong sach giao khoa do minh ko noi chi tiet)
=>goc NKF=goc MKF(2 goc nt chan 2 cung = nhau)
=> phan giac ....
c,
CO GOC FOM=GOC FON (2 goc o tam chan 2 cung = nhau )=>goc NOM =80
\(l_{MFN}\) =....(dung may cong thuc trong sach giao khoa ay)
dien h OMFN cung dung cong thuc trong sgk tu tim hieu nhe moi nho lau

1: góc AKB=1/2*180=90 độ
góc AKC+góc AEC=180 độ
=>AKCE nội tiếp
2: Xet ΔBMC và ΔBKM có
góc BMC=góc BKM
góc MBC chung
=>ΔBMC đồng dạng với ΔBKM
=>BM/BK=BC/BM
=>BM^2=BK*BC

OM^2+ON^2=MN^2 và OM=ON
=>ΔOMN vuông cân tại O
ΔOMN cân tại O có OH là đường cao
nên OH là phân giác của góc MON
=>góc MOA=22,5 độ
=>góc MOB=157,5 độ
=>góc OMB=11,25 độ
=>góc HMB=56,25 độ
cos HMB=HM/MB
=>MB\(\simeq\)1,27R
=>MA\(\simeq1,55R\)


