Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có m = 1 e 2 p − q = e q − 2 p , n = e p − 2 q .
Vì m>n nên q − 2 p > p − 2 q ⇔ q > p .

15.
Ta có \(a+b+c+ab+bc+ac=6\)
Mà \(ab+bc+ac\le\left(a+b+c\right)^2\)
=> \(\left(a+b+c\right)^2+\left(a+b+c\right)-6\ge0\)
=> \(a+b+c\ge3\)
\(A=\frac{a^4}{ab}+\frac{b^4}{bc}+\frac{c^4}{ac}\ge\frac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ac}\ge a^2+b^2+c^2\ge\frac{1}{3}\left(a+b+c\right)^2\ge3\)(ĐPCM)
Bài 18, Đặt \(\left(a^2-bc;b^2-ca;c^2-ab\right)\rightarrow\left(x;y;z\right)\) thì bđt trở thành
\(x^3+y^3+z^3\ge3xyz\)
\(\Leftrightarrow x^3+y^3+z^3-3xyz\ge0\)
\(\Leftrightarrow\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\ge0\)
\(\Leftrightarrow\frac{1}{2}\left(x+y+z\right)\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]\ge0\)
Vì \(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)nên ta đi chứng minh \(x+y+z\ge0\)
Thật vậy \(x+y+z=a^2-bc+b^2-ca+c^2-ab\)
\(=\frac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]\ge0\)(đúng)
Tóm lại bđt được chứng minh
Dấu "=": tại a=b=c

\(_{\frac{p}{m-1}=\frac{m+n}{p}\Rightarrow p^2=\left(m-1\right)\times\left(m+n\right)\Rightarrow p^2=m^2+m\times n-m-n\Rightarrow p^2=m^2+m\times n-m-2\times n}\)
Vậy A\(=p^2-n=m^2+m\times n-m-2\times n\)

Bạn tham khảo bài của Đinh Tuấn Việt ở Câu hỏi của Tài Nguyễn Tuấn - Chuyên mục hỏi đáp - Giúp tôi giải toán. - Học toán với OnlineMath
\(m;n\in N\Rightarrow m;n\ge0\)
\(p\) là số nguyên tố
Thỏa mãn \(\frac{p}{m-1}=\frac{m+n}{p}\Leftrightarrow p^2=\left(m-1\right)\left(m+n\right)\)
Do \(\left(m-1\right)\) và \(\left(m+n\right)\) là các ước nguyên dương của \(p^2\)
Lưu ý: \(m-1< m+n\left(1\right)\)
Vì \(p\) là số nguyên tố nên \(p^2\)chỉ có các ước nguyên dương là \(1,p\) và \(p^2(2)\)
Từ \((1)\) và \(\left(2\right)\) ta có \(m-1=1\) và \(m+n=p^2\)
\(\Rightarrow m=2\) và\(2+n=p^2\)
Vậy\(A=p^2-n=2\)

cho 2014=2013+1 thay vào ta có:\(B=x^{2013}-\left(2013+1\right)x^{2012}+\left(2013+1\right)x^{2011}-...-\left(2013+1\right)x^2+\left(2013+1\right)x-1\)
\(=x^{2013}-\left(x+1\right)x^{2012}+\left(x+1\right)x^{2011}-...-\left(x+1\right)x^2+\left(x+1\right)x-1\)
\(=x^{2013}-x^{2013}-x^{2012}+x^{2012}+x^{2011}-...-x^3-x^2+x^2+x-1\)
\(=x-1=2013-1=2012\)
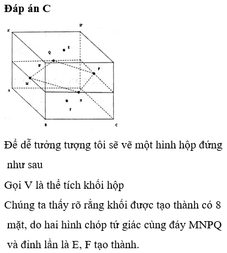

Đáp án D
Ta có m = 1 e 2 p − q = e q − 2 p , n = e p − 2 q .
Vì m > n nên q − 2 p > p − 2 q ⇔ q > p .