Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm của \(\left(d\right)\) và \(\left(P\right)\) là:
\(x^2=2mx+3\Leftrightarrow x^2-2mx-3=0\) (1)
Phương trình (1) có hệ số \(a.c=1.\left(-3\right)=-3< 0\) nên (1) luôn có hai nghiệm phân biệt \(x_1,x_2\).
Theo hệ thức Viete ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-3\end{matrix}\right.\)
Ta có: \(\left|x_1\right|+3\left|x_2\right|=6\)
Ta có hệ:
\(\left\{{}\begin{matrix}x_1x_2=-3\\\left|x_1\right|+3\left|x_2\right|=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{3}{x_2}\\\left|\dfrac{3}{x_2}\right|+3\left|x_2\right|=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{3}{x_2}\\x_2^2-2\left|x_2\right|+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2=-1,x_1=3\\x_2=1,x_1=-3\end{matrix}\right.\)
Với \(x_1=3,x_2=-1\Rightarrow x_1+x_2=2\Rightarrow m=1\).
Với \(x_1=-3,x_2=1\Rightarrow x_1+x_2=-2\Rightarrow m=-1\)
Phương trình hoành độ giao điểm của và là:
(1)
Phương trình (1) có hệ số nên (1) luôn có hai nghiệm phân biệt .
Theo hệ thức Viete ta có:
Ta có:
Ta có hệ:
Với .
Với

a, Xét hoành độ giao điểm của P và d ta có:
x2 = 3x + m2 - 2
\(\Delta=b^2-4ac=4m^2+1>0\) ∀x
=> d luôn cắt P tại hai điểm phân biệt.

Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình:
\(x^2=ax+3\)
\(\Leftrightarrow x^2-ax-3=0\)
có \(\Delta=\left(-a\right)^2-4.1.\left(-3\right)=a^2+12\ge12>0\forall a\)
=> phương trình luôn có 2 nghiệm phân biệt x1,x2
theo hệ thức Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=a\left(1\right)\\x_1x_2=-3\left(2\right)\end{matrix}\right.\)
mà \(x_1+2x_2=3\left(3\right)\)
Từ (1) và (3) ta có hệ:
\(\left\{{}\begin{matrix}x_1+x_2=a\\x_1+2x_2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=3-a\\x_1+x_2=a\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_1=2a-3\\x_2=3-a\end{matrix}\right.\)
Theo (2) ta có:
\(x_1x_2=-3\Leftrightarrow\left(2a-3\right)\left(3-a\right)=-3\)
\(\Leftrightarrow6a-2a^2-9+3a=-3\)
\(\Leftrightarrow2a^2-9a+6=0\)
\(\Delta=\left(-9\right)^2-4.2.6=81-48=33>0\)
\(\Rightarrow a_1=\dfrac{9+\sqrt{33}}{4};a_2=\dfrac{9-\sqrt{33}}{4}\)
Vậy \(a\in\left\{\dfrac{9+\sqrt{33}}{4};\dfrac{9-\sqrt{33}}{4}\right\}\)để x1+2x2=3

b: Phương trình hoành độ giao điểm là:
\(x^2-\left(m-1\right)x-m=0\)
\(\text{Δ}=\left(m-1\right)^2-4\cdot1\cdot\left(-m\right)=\left(m+1\right)^2>=0\)
Do đó: Phương trình luôn có hai nghiệm
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1-x_2=2\\x_1+x_2=m-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1=m+1\\x_1-x_2=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{1}{2}m+\dfrac{1}{2}\\x_2=\dfrac{1}{2}m+\dfrac{1}{2}-2=\dfrac{1}{2}m-\dfrac{3}{2}\end{matrix}\right.\)
Theo đề, ta có: \(x_1x_2=-m\)
\(\Leftrightarrow-m=\left(\dfrac{1}{2}m+\dfrac{1}{2}\right)\left(\dfrac{1}{2}m-\dfrac{3}{2}\right)\)
Đến đây bạn chỉ cần giải phương trình bậc hai là xong

Phương trình hoành độ giao điểm d và (P):
\(-2x^2=x-m\Leftrightarrow2x^2+x-m=0\) (1)
(d) cắt (P) tại 2 điểm pb khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta=1+8m>0\Leftrightarrow m< -\dfrac{1}{8}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{1}{2}\\x_1x_2=-\dfrac{m}{2}\end{matrix}\right.\)
\(x_1+x_2=x_1x_2\Leftrightarrow-\dfrac{1}{2}=-\dfrac{m}{2}\Leftrightarrow m=1\)

b. Phương trình hoành độ giao điểm:
\(x^2=4x-m\Leftrightarrow x^2-4x+m=0\) (1)
d cắt (P) tại 2 điểm phân biệt khi và chỉ khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta'=4-m>0\Rightarrow m< 4\)
Khi đó kết hợp hệ thức Viet và điều kiện đề bài:
\(\left\{{}\begin{matrix}x_1+x_2=4\\2x_1+x_2=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=4\\x_1=-9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-9\\x_2=13\end{matrix}\right.\)
Mà \(x_1x_2=m\)
\(\Rightarrow m=-9.13=-117\)
a) Thay m=6 vào (d), ta được: y=4x-6
Phương trình hoành độ giao điểm của (P) và (d) là:
\(2x^2=4x-6\)
\(\Leftrightarrow2x^2-4x+6=0\)
\(\text{Δ}=\left(-4\right)^2-4\cdot2\cdot6=16-48=-32\)(loại)
Vì Δ<0 nên phương trình vô nghiệm
Vậy: Khi m=6 thì (P) và (d) không có điểm chung





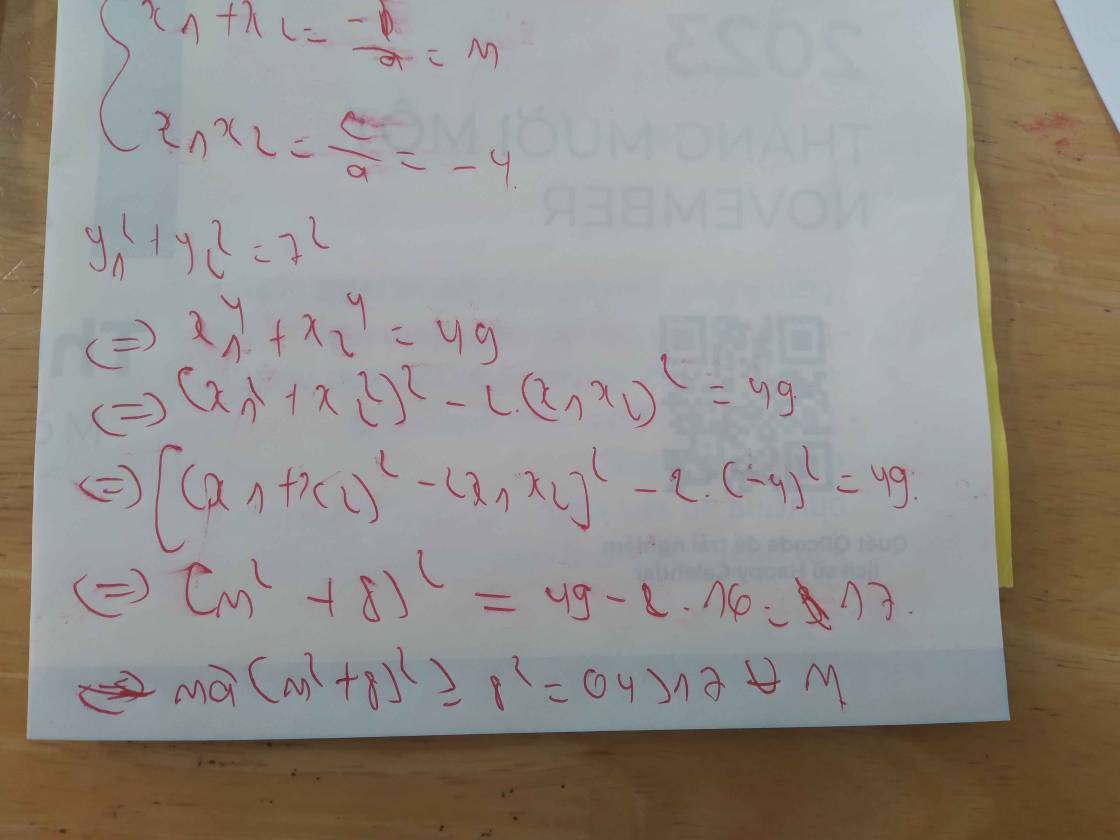

Chào bạn! Mình hướng dẫn nha!
Do x1 và x2 là hoành độ giao điểm của (d) và (p)
=> x1 và x2 là 2 nghiệm của pt x^2 = ax +3
=> x^2 -ax -3 =0
Do pt có 2 nghiệm phân biệt nên đen-ta >0
=> a^2 +12 >0 (luôn đúng do a^2 >=0)
Ta có x1 +2x2 =3 => x1 +x2 = 3- x2 Mà x1 +x2 =a (theo vi-ét)
=> a = 3 -x2 => a = 3 - [a +căn(đen-ta)]/2 (vì [a +căn(đen-ta)]/2 là nghiệm x2 của pt)
=> 2a = 6 -a +căn(đen-ta)
=> 3a -6 = căn(đen-ta) Bình phương 2 vế:
=> 9a^2 - 36a +36 = đen-ta = a^2 +12
=> 8a^2 -36a + 24 =0 => 2x^2 -9x +6 =0
Bấm máy => a ~~ 3,69 hoặc a ~~ 0,81 (lưu ý: ~~ là gần bằng)
Vậy với a = 3,69 hoặc a =0,81 thì thỏa mãn yêu cấu bài toán!
Thế thôi, chúc bạn thành công nha!!!
K hiểu phần cuối bạn ơi