
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$B=\frac{3-4n}{2n+1}=\frac{5-2(2n+1)}{2n+1}=\frac{5}{2n+1}-2$
Để $B$ lớn nhất thì $\frac{5}{2n+1}$ lớn nhất
Điều này xảy ra khi $2n+1$ là số dương nhỏ nhất.
Với $n\in\mathbb{Z}$, $2n+1$ đạt giá trị dương nhỏ nhất bằng $1$
$\Rightarrow B_{\max}=\frac{5}{1}-2=3$

\(A=\frac{4n+1}{2n+3}=\frac{2\left(2n+3\right)-5}{2n+3}=2-\frac{5}{2n+3}\)
Vậy để A nguyên thì 2n+3\(\in\)Ư(5)
Mà Ư(5)={1;-1;5;-5}
=>2n+3={1;-1;5;-5}
Ta có bảng sau
| 2n+3 | 1 | -1 | 5 | -5 |
| n | -1 | -2 | 1 | -4 |
Vậy n={-1;-2;-4;1}
Vì \(\frac{4n+1}{2n+3}\) là số nguyên nên \(4n+1⋮2n+3\)
\(\Rightarrow4n+6-5⋮2n+3\)
\(\Rightarrow2\left(2n+3\right)-5⋮2n+3\)
\(\Rightarrow5⋮2n+3\)
\(\Rightarrow2n+3\in\left\{\pm1;\pm5\right\}\)
Nếu 2n + 3 = 1 thì n = -1
Nếu 2n + 3 = -1 thì n = -2
Nếu 2n + 3 = 5 thì n = 1
Nếu 2n + 3 = -5 thì n = -4
Vậy \(n\in\left\{-1;-2;1;-4\right\}\)

Ta có:\(\frac{10}{5n-3}=\frac{2.\left(5n-3\right)+6}{5n-3}=2+\frac{6}{n-3}\)
Suy ra:6 chia hết cho n-3
Hoặc n-3\(\in\)Ư(6)
Vậy Ư(6) là:(1,2,3,6)
Do đó ta có bảng sau:
| 5n-3 | 1 | 2 | 3 | 6 |
| 5n | 4 | 5 | 6 | 9 |
| n | ko TM | 1 | ko TM | ko TM |
Vậy n=1
Giải:
Để B thuộc Z thì 10n chia hết cho 5n - 3
\(10n⋮5n-3\)
\(\Rightarrow\left(10n-6\right)+6⋮5n-3\)
\(\Rightarrow2\left(5n-3\right)+6⋮5n-3\)
\(\Rightarrow6⋮5n-3\)
\(\Rightarrow5n-3\in\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
+) \(5n-3=1\Rightarrow n=\frac{4}{5}\) ( loại )
+) \(5n-3=-1\Rightarrow n=\frac{2}{5}\) ( loại )
+) \(5n-3=2\Rightarrow n=1\) ( chọn )
+) \(5n-3=-2\Rightarrow n=\frac{1}{5}\) ( loại )
+) \(5n-3=3\Rightarrow n=\frac{6}{5}\) ( loại )
+) \(5n-3=-3\Rightarrow n=0\) ( chọn )
+) \(5n-3=6\Rightarrow n=\frac{9}{5}\) ( loại )
+) \(5n-3=-6\Rightarrow n=\frac{-3}{5}\) ( loại )
Vì 0 < 1 nên n = 1 để B có giá trị lớn nhất
Vậy n = 1
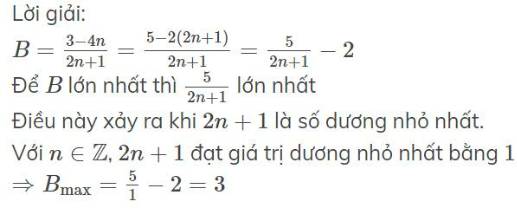
cô giải kiểu delta lớp 9 đúng k ạ