`B4:`

`a)` Thay `x=3` vào ptr:

  `3^3-3^2-9.3-9m=0<=>m=-1`

`b)` Thay `m=-1` vào ptr có: `x^3-x^2-9x+9=0`

        `<=>x^2(x-1)-9(x-1)=0`

        `<=>(x-1)(x-3)(x+3)=0<=>[(x=1),(x=+-3):}`

`B5:`

`a)` Thay `x=-2` vào có: `(-2)^3-(m^2-m+7).(-2)-3(m^2-m-2)=0`

    `<=>-8+2m^2-2m+14-3m^2+3m+6=0`

   `<=>-m^2+m+12=0<=>(m-4)(m+3)=0<=>[(m=4),(m=-3):}`

`b)`

`@` Với `m=4` có: `x^3-(4^2-4+7)x-3(4^2-4-2)=0`

      `<=>x^3-19x-30=0`

      `<=>x^3-5x^2+5x^2-25x+6x-30=0`

      `<=>(x-5)(x^2+5x+6)=0`

      `<=>(x-5)(x+2)(x+3)=0<=>[(x=5),(x=-2),(x=-3):}`

`@` Với `m=-3` có: `x^3-[(-3)^2-(-3)+7]x-3[(-3)^2-(-3)-2]=0`

   `<=>x^3-19x-30=0<=>[(x=5),(x=-2),(x=-3):}`

\(\left(x^2+x\right)^2+4\left(x^2+x\right)=12\)

đặt \(\left(x^2+x\right)=t\)  ta có 

\(t^2+4t-12=0\)

\(\Leftrightarrow t^2+6t-2t-12=0\)

\(\Leftrightarrow t\left(t+6\right)-2\left(t+6\right)=0\)

\(\Leftrightarrow\left(t-2\right)\left(t+6\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}t-2=0\\t+6=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}t=2\\t=-6\end{cases}}\)

khi đó giả lại biến \(\left(x^2+x\right)\) rồi làm như bình thường 

a: Khi k=0 thì PT sẽ là:

9x^2-25=0

=>x=5/3 hoặc x=-5/3

b: Thay x=-1 vào pt, ta sẽ được:

-k^2+2k+9-25=0

=>-k^2+2k-16=0

=>\(k\in\varnothing\)

Thay x = 1/2 vào phương trình, ta có:

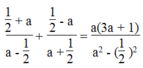
ĐKXĐ: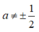 

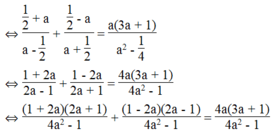
⇔ (1 + 2a)(2a + 1) + (1 – 2a)(2a – 1) = 4a(3a + 1)

⇔ 2a + 1 + 4 a 2  + 2a + 2a – 1 – 4 a 2  + 2a = 12 a 2  + 4a

⇔ 12 a 2  – 4a = 0 ⇔ 4a(3a – 1) = 0 ⇔ 4a = 0 hoặc 3a – 1 = 0

⇔ a = 0 (thỏa mãn) hoặc a = 1/3 (thỏa mãn)

Vậy khi a = 0 hoặc a = 1/3 thì phương trình  x + a a - x + x - a a + x = a 3 a + 1 a 2 - x 2  có nghiệm x = 1/2

Bài này có trong sbt toán 8 tập 2 mà!

Minh ko biet lam