Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(3x^2+5x-6=0\\ \Delta=5^2-4.3.\left(-6\right)=97\\ \Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{-5+\sqrt{97}}{2}\\x_2=\dfrac{-5-\sqrt{97}}{2}\end{matrix}\right.\)
\(\left(x_1-2x_2\right).\left(2x_1-x_2\right)=2x^2_1-4x_1x_2+2x_2^2\)
\(=2.\left(\dfrac{-5+\sqrt{97}}{2}\right)^2-4.\left(\dfrac{-5+\sqrt{97}}{2}\right).\left(\dfrac{-5-\sqrt{97}}{2}\right)+2.\left(\dfrac{-5-\sqrt{97}}{2}\right)^2\\ =\left(\dfrac{-5+\sqrt{97}}{2}\right)^2-2.\left(\dfrac{-5+\sqrt{97}}{2}\right).\left(\dfrac{-5-\sqrt{97}}{2}\right)+\dfrac{\left(-5-\sqrt{97}\right)^2}{2^2}\\ =\left(\dfrac{-5+\sqrt{97}}{2}-\dfrac{-5-\sqrt{97}}{2}\right)^2\\ =\left(\dfrac{-5+\sqrt{97}+5+\sqrt{97}}{2}\right)^2\\ =\left(\dfrac{2\sqrt{97}}{2}\right)^2\\ =\left(\sqrt{97}\right)^2=97\)

a) Do a = 3; c = -7 nên a và c trái dấu
Vậy phương trình luôn có hai nghiệm phân biệt
b) Theo Viét ta có:
x₁ + x₂ = -4/3
x₁x₂ = -7/3
Ta có:
2x₁ - (x₁ - x₂ - x₁x₂)
= 2x₁ - x₁ + x₂ + x₁x₂
= x₁ + x₂ + x₁x₂
= -4/3 - 7/3
= -11/3
\(3x^2+4x-7=0\)
\(a,\) Để pt có 2 nghiệm phân biệt thì \(\Delta>0\Rightarrow4^2-4.3.\left(-7\right)=100>0\)
Vậy pt có 2 nghiệm phân biệt \(x_1,x_2\)
\(b,\)Theo Vi-ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{4}{3}\\x_1x_2=\dfrac{c}{a}=-\dfrac{7}{3}\end{matrix}\right.\)
Ta có : \(2x_1-\left(x_1-x_2-x_1x_2\right)\)
\(=2x_1-x_1+x_2-x_1x_2\)
\(=x_1+x_2-x_1x_2\)
\(=-\dfrac{4}{3}-\left(-\dfrac{7}{3}\right)\)
\(=-\dfrac{4}{3}+\dfrac{7}{3}\)
\(=\dfrac{3}{3}=1\)
Vậy giá trị của biểu thức là \(1\)

Ptr có: `\Delta' = b'^2-ac=(-1)^2-(-4)=5 > 0`
`=>` Ptr có `2` nghiệm pb
`=>` Áp dụng Vi-ét: `{(x_1+x_2=[-b]/a=2),(x_1.x_2=c/a=-4):}`
Có: `T=x_1(x_1-2x_2)+x_2(x_2-2x_1)`
`=>T=x_1 ^2 - 2x_1.x_2+x_2 ^2 - 2x_1.x_2`
`=>T=(x_1+x_2)^2-6x_1.x_2`
`=>T=2^2-6(-4)=28`

a) \(x^2+2\left(m-1\right)x-6m-7=0\)\(0\)
\(\left(a=1;b=2\left(m-1\right);b'=m-1;c=-6m-7\right)\)
\(\Delta'=b'^2-ac\)
\(=\left(m-1\right)^2-1.\left(-6m-7\right)\)
\(=m^2-2m+1+6m+7\)
\(=m^2+4m+8\)
\(=m^2+2.m.2+2^2+4\)
\(=\left(m+2\right)^2+4>0,\forall m\)
Vì \(\Delta'>0\) nên phương trình ( 1 ) luôn có 1 nghiệm phân biệt với mọi m

\(2x^2-6x-3=0\)
\(\Delta'=3^2+3.2=15>0\)
⇒ Phương trình có hai nghiệm phân biệt.
Theo hệ thức viét có : \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=-\dfrac{3}{2}\end{matrix}\right.\)
Ta có : \(A=x_1^2x_2^2-2x_1-2x_2=\left(x_1x_2\right)^2-2\left(x_1+x_2\right)=\left(-\dfrac{3}{2}\right)^2-2.3=-\dfrac{15}{4}\)
Vậy \(A=-\dfrac{15}{4}\) thì thỏa mãn điều kiện bài ra.

PT có 2 nghiệm phân biệt `<=> \Delta>0`
`<=>3^2-4m>0`
`<=>m<9/4`
Viet:
`x_1+x_2=-3` (1)
`x_1x_2=m` (2)
Theo đề: `x_2=2x_1 <=> 2x_1-x_2=0` (3)
Từ (1) và (3) ta có hệ: \(\left\{{}\begin{matrix}x_1+x_2=-3\\2x_1-x_2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-1\\x_2=-2\end{matrix}\right.\)
Thay vào (2): `(-1).(-2) = m <=> m=2`
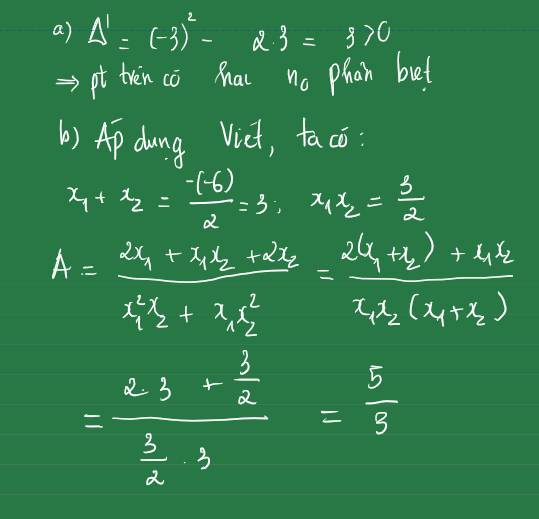
ai giúp em với ạ 😥