Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi z=a+bi a ∈ ℝ , b ∈ ℝ , ta có:
![]()
![]()
![]()
![]()
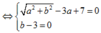
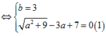
Giải (1) ta có:
![]()
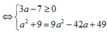
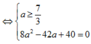
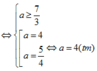
Do đó a=4; b=3; ⇒ z=4+3i
Khi đó
![]()
=1-4-3i+16+24i-9=4-21i
Vậy w = 4 2 + - 21 2 = 457 .
Chọn đáp án D.

Gọi z = a + bi với a , b ∈ ℝ
Khi đó phương trình z + z 1 + i + z - z 2 + 3 i = 4 - i trở thành:
2 a 1 + i + 2 b 2 + 3 i = 4 - i ⇔ 2 a + 4 b + 2 a + 6 b i = 4 - i
Do đó:
2 a + 4 b = 4 2 a + 6 b = - 1 a = 1 2 b = - 1 2 ⇒ z = 1 2 - 1 2 i
Ta có: w = z 3 + z + 1 z 2 + 1 - = z + 1 z 2 + 1 Thay 1 2 - 1 2 i vào ta được:
w = 1 2 - 1 2 i + 1 1 2 - 1 2 i 2 + 1 = 1 2 - 1 2 i + 1 - 1 2 i + 1 = 13 10 - 1 10 i
Suy ra w = 13 10 2 + - 1 10 2 = 170 10
Đáp án A

Đáp án A
Phương pháp: Cho z1, z2 là hai số phức bất kì, khi đó | z1.z2 | = |z1|.|z2|
Cách giải: Ta có:
![]()
![]()
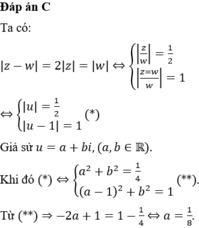


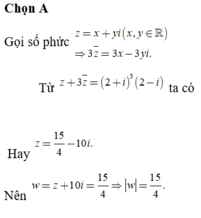

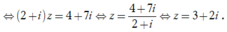
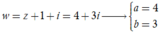
Đáp án D