Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

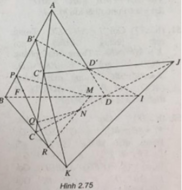
a) Chú ý rằng I, J, K thẳng hàng vì chúng cùng thuộc giao tuyến của hai mặt phẳng (CBD) và (C'B'D')
b) 4. Vì 4 điểm không đồng phẳng sẽ tạo nên 1 tứ diện => có 4 mặt

Có thể bỏ chút thời gian chỉ mình cách làm được không :<

\(BC\) \(\subset\)\(\left(SBC\right)\)
Tìm giao tuyến của của \(\left(OMN\right)\)và \(\left(SBC\right)\):
\(N\)là điểm chung thứ nhất
Ta có : \(MO\)\(\subset\)\(\left(AMO\right)\)\(\equiv\)\(\left(SAH\right)\)với \(H=AO\)\(\cap\) \(BC\)
\(\left(SAH\right)\)\(\cap\) \(\left(SBC\right)\)= \(SH\)
Trong \(\left(SAH\right)\): \(MO\)\(\cap\) \(SH\)= \(K\)
\(K\)là điểm chung thứ 2.
Vậy \(\left(OMN\right)\)\(\cap\)\(\left(SBC\right)\)= \(NK\)
Trong \(\left(SBC\right):\)\(NK\)\(\cap\)\(BC\)= \(P\)
Vậy \(\left(OMN\right)\)\(\cap\) \(BC\)= \(P\)
Ta có N thuộc (OMN)
C thuộc đường thẳng BC
Mà N trùng với C => N là giao điểm của (OMN) và BC

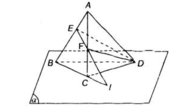
a) E ∈ AB mà AB ⊂ (ABC)
⇒ E ∈ (ABC)
F ∈ AC mà AC ⊂ (ABC)
⇒ F ∈ (ABC)
Đường thẳng EF có hai điểm E, F cùng thuộc mp(ABC) nên theo tính chất 3 thì EF ⊂ (ABC).
b) I ∈ BC mà BC ⊂ (BCD) nên I ∈ (BCD) (1)
I ∈ EF mà EF ⊂ (DEF) nên I ∈ (DEF) (2)
Từ (1) và (2) suy ra I là điểm chung của hai mặt phẳng (BCD) và (DEF).

Người vô văn hoá là bn đấy !!! @7D18
Không tả lời linh tinh nha