Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAMB và ΔCMD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔAMB=ΔCMD
Suy ra: AB=CD
b: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: \(\widehat{ABC}=\widehat{DCB}=50^0\)

UKM THÌ CÓ BÀI TỰA VẬY BẠN SO ĐC CHỨ
a) Xét AIM và BIC có:IA = IB (do I là trung điểm của AB);AIM BIC(hai góc đối đỉnh);IM = IC (giảthiết).Do đó AIM = BIC (c.g.c)Suy ra AM = BC (hai cạnh tương ứng) và MAI CBI(hai góc tương ứng) Mà MAI, CBIlà hai góc ởvịtrí so le trong nên AM // BC.b) Xét ANE và CBE có:EA = EC (do E là trung điểm của AC);AEN CEB(hai góc đối đỉnh);EN= EB(giảthiết).Do đó ANE = CBE (c.g.c)Suy ra NAE BCE(hai góc tương ứng)Mà NAE, BCElà hai góc ởvịtrí so le trong nên AN// BC.c) Ta có AM // BC (theo câu a) và AN // BC (theo câu b)Do đó qua điểm A có hai đường thẳng song song với BC nên theo tiên đềEuclid, hai đường thẳng AM và AN trùng nhau hay ba điểm A, M, N thẳng hàng.Lại có ANE = CBE (theo câu b) nên AN = CB (hai cạnh tương ứng)Mặt khác AM = BC (theo câu a)Do đó AM = AN (cùng bằng BC) Mà ba điểm A, M, N thẳng hàng nên A là trung điểm của MN.a: Xét ΔAMB và ΔCMD có
MA=MC
góc AMB=góc CMD
MB=MD
Do đó: ΔAMB=ΔCMD
b: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
nên ABCD là hình bình hành
=>AB//CD và AB=CD
c: Xét tứ giác AKBC có
N là trung điểm chung của AB và KC
nên AKBC là hình bình hành
=>AK//BC
mà AD//BC
nên D,A,K thẳng hàng

a: Đề sai rồi bạn
b: Xét ΔAMB và ΔCME có
MA=MC
\(\widehat{AMB}=\widehat{CME}\)
MB=ME
Do đó: ΔAMB=ΔCME

a) M là trung điểm AC(gt) => AM=CM
Xét tg BMC và tg DMA ta có:
- BM=DM(gt)
- ^BMC=^DMA(đối đỉnh)
- MC=MA(cmt)
=> tg BMC=tg DMA(c.g.c)
b) tg BMC=tg DMA(câu a)
=> ^MBC=^MDA (2 góc tương ứng)
Mà 2 góc này so le trong => AD//BC
Lại có: AH vuông góc BC(gt)
=> AH vuông góc AD (quan hệ //, vuông góc)
c) Ta có: AH vuông góc AD( câu b)
CK vuông góc AD(gt)
=> AH//CK(1)
Mà AD//BC(câu b) hay AK//CH (2)
Từ (1),(2) => AH=CK; AK=CH(3)
Tg BMC= tg DMA (câu a) => BC=DA(4)
Lại có: BC=CH + BH(5)
DA= AK + DK(6)
Từ (3)(4)(5)(6) => BH=DK
Có: ^MBC=^MDA(câu b) hay ^MBH=^MDK
Xét tg BMH và tg DMK có:
- BM=DM(gt)
- ^MBH=^MDK (cmt)
- BH=DK (cmt)
=> tg BMH=tg DMK (c.g.c)
=> ^BMH=^DMK
=>^BMH + ^BMK =^DMK+^BMK
Hay: ^HMK=^BMD=180°
=> H, M, K thẳng hàng

a: Xét ΔAMB và ΔCMD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD
Do đó: ΔAMB=ΔCMD
b: ta có: ΔAMB=ΔCMD
=>\(\widehat{MAB}=\widehat{MCD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
c: Xét ΔIBM và ΔKDM có
IB=KD
\(\widehat{IBM}=\widehat{KDM}\)(hai góc so le trong, AB//CD)
BM=MD
Do đó: ΔIBM=ΔKDM
=>\(\widehat{IMB}=\widehat{KMD}\)
mà \(\widehat{IMB}+\widehat{IMD}=180^0\)(hai góc kề bù)
nên \(\widehat{KMD}+\widehat{IMD}=180^0\)
=>I,M,K thẳng hàng

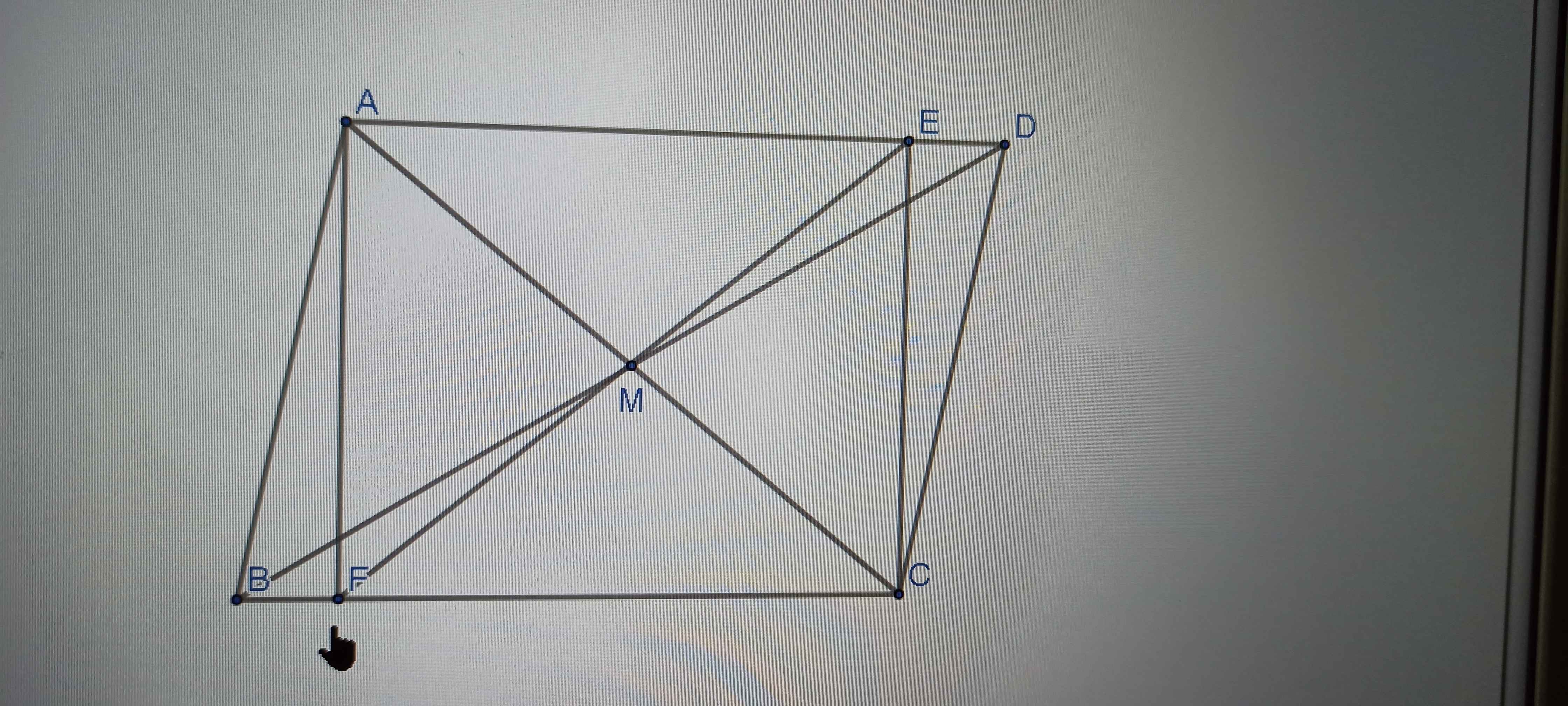
Câu C bạn cm AFCE là hình chữ nhật , FE là đường chéo => E,F,M thẳng hàng vì 2 đường chéo hình chữ nhật đi qua trung điểm của mỗi đường.