Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a)`
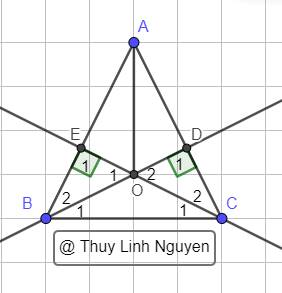
Có `Delta ABC` cân tại `A(g t)`
`=>hat(ABC)=hat(ACB)`
`=>hat(EBC)=hat(DCB)`
Xét `Delta BEC` và `Delta CDB` có :
`{:(hat(E_1)=hat(D_1)(=90^0)),(BC-chung),(hat(EBC)=hat(DCB)(cmt)):}}`
`=>Delta BEC=Delta CDB(c.h-g.n)`
`=>CE=BD` ( 2 cạnh tương ứng )( dpcm )
`b)`
Có `Delta BEC=Delta CDB(cmt)`
`=>hat(C_1)=hat(B_1)` ( 2 góc tương ứng )
`=>Delta BOC` cân tại `O`
`=>OB=OC`(dpcm)
Xét `Delta OEB` và `Delta ODC` có :
`{:(hat(E_1)=hat(D_1)(=90^0)),(OB=OC(cmt)),(hat(O_1)=hat(O_2)(doi.di nh)):}}`
`=>Delta OEB=Delta ODC(c.h-g.n)`
`=>OE=OD`( 2 cạnh tương ứng )(dpcm)
`c)`
Có `Delta ABC` cân tại `A(g t)`
`=>AB=AC`
`=>A in ` trung trực của `Delta ABC(1)`
Có `OB=OC(cmt)`
`=>O in` trung trực của `Delta ABC(2)`
Từ `(1)` và `(2)=>OA` là trung trực `Delta ABC`
mà `Delta ABC` cân tại `A`
Nên `OA` là phân giác `hat(BAC)` (dpcm)

a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó: ΔEBC=ΔDCB
Suy ra: EC=DB
b: Xét ΔOEB vuông tại E và ΔODC vuông tại D có
EB=DC
\(\widehat{EBO}=\widehat{DCO}\)
Do đó:ΔOEB=ΔODC
c: Ta có: ΔOEB=ΔODC
nên OB=OC
Xét ΔAOB và ΔAOC có
AO chung
OB=OC
AB=AC
Do đó: ΔAOB=ΔAOC
Suy ra: \(\widehat{BAO}=\widehat{CAO}\)
hay AO là tia phân giác của góc BAC

a) t/g ABC cân tại A
=> ABC = ACB ( tính chất tam giác cân)
Xét t/g DCB vuông tại D và tam giác EBC vuông tại E có:
BC là cạnh chung
DCB = EBC (cmt)
Do đó, t/g DCB = t/g EBC ( cạnh huyền - góc nhọn)
=> BD = CE (2 cạnh tương ứng) (đpcm)
b) t/g DCB = t/g EBC (câu a)
=> CD = BE (2 cạnh tương ứng)
DBC = ECB (2 góc tương ứng)
Mà ABC = ACB (câu a)
=> ABC - DBC = ACB - ECB
=> ABD = ACE
Xét t/g EBO vuông tại E và t/g DCO vuông tại D có:
BE = CD (cmt)
EBO = DCO (cmt)
Do đó, t/g EBO = t/g DCO ( cạnh góc vuông và góc nhọn kề)
=> OB = OC (2 cạnh tương ứng) (1)
OE = OD (2 cạnh tương ứng) (2)
Từ (1) và (2) => đpcm
c) Dễ thấy, t/g AOC = t/g AOB (c.c.c)
=> OAC = OAB (2 góc tương ứng)
=> AO là phân giác CAB (đpcm)
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có:
AB = AC (gt)
Góc A chung
=> ΔABD = ΔACE ( cạnh huyền - góc nhọn )
=> BD = CE ( 2 cạnh tương ứng )
b) Vì ΔABD = ΔACE nên góc ABD = ACE ( 2 góc tương ứng ) và AD = AE ( 2 cạnh tương ứng )
Ta có: AD + DC = AC
AE + EB = AB
mà AD = AE (cm trên); AC = AB (gt)
=> DC = EB
Xét ΔEOB và ΔDOC có:
góc ABD = ACE (cm trên)
EB = DC (cm trên)
góc OEB = ODC (= 90)
=> ΔEOB = ΔDOC (g.c.g)
=> OE = OD ( 2 cạnh tương ứng ) ; OB = OC ( 2 cạnh tương ứng )
c) Do ΔEOB = ΔĐỌC nên EO = DO ( 2 cạnh tương ứng )
Xét ΔAOE vuông tại E và ΔAOD vuông tại D có:
OE = DO ( cm trên )
AE = AD (câu b)
=> ΔAOE = ΔAOD ( cạnh góc vuông )
=> góc OAE = OAD ( 2 góc tương ứng )
Do đó AO là tia phân giác của góc EAD hay AO là tia pg của góc BAC.
Chúc học tốt Cathy Trang



đéo biết làm
tự vẽ hình nha
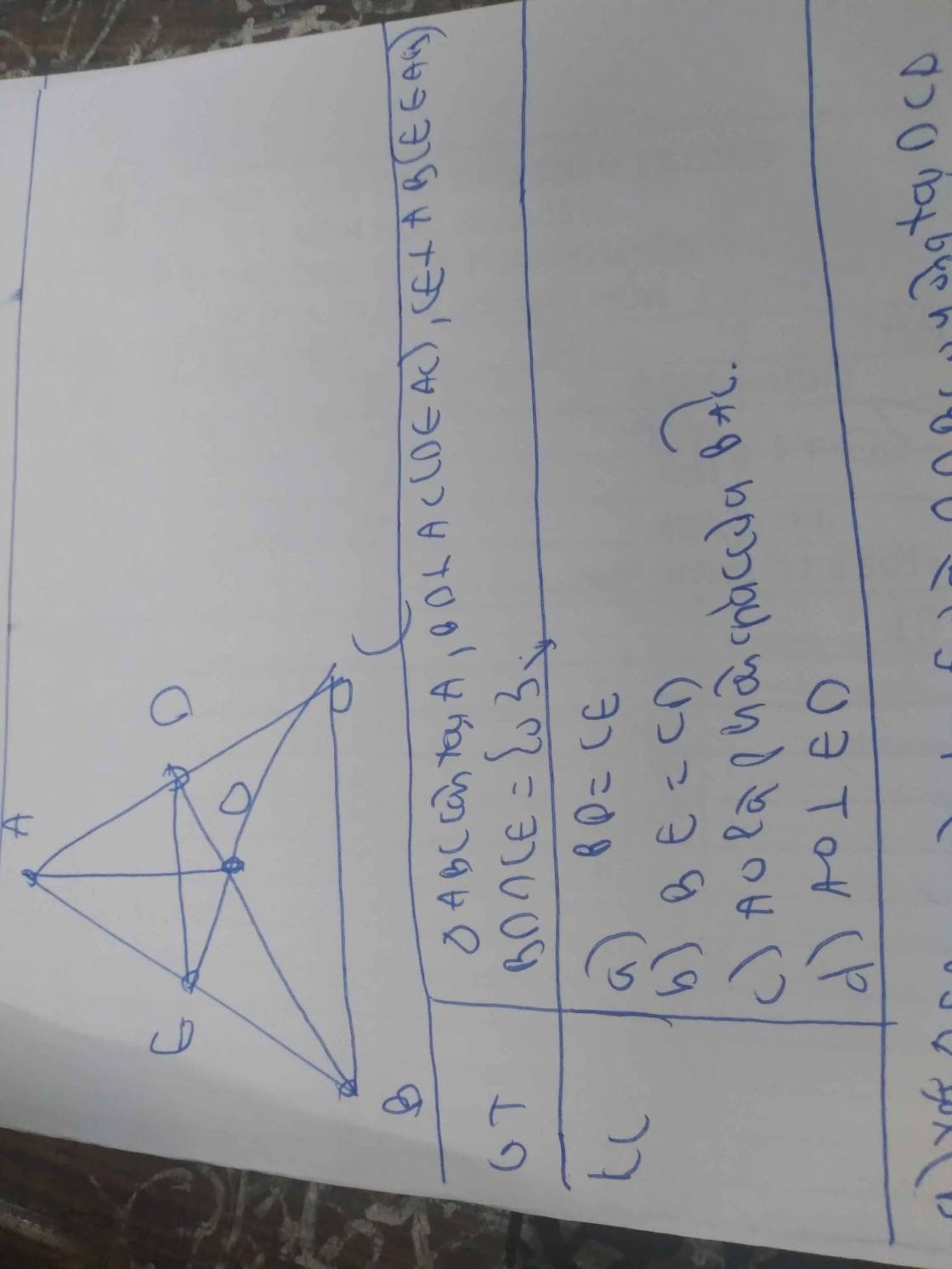
a, Xét tg ABD và tg ACE có:
AB=AC (gt)
góc A chung
góc ADB = góc AEC (=90)
=>tg ABD = tg ACE (ch-gn)
=>BD=CE (1)
b, Xét tg OAD và tg OAE có;
AD=AE (tg ABD = tg ACE)
OA chung
góc ODA = góc OED (=90)
=>tg OAD = tg OAE (ch-cgv)
=>OD=OE (2)
Từ (1),(2) => BD - OD = CE - OE hay OB = OC
c, từ tg OAD = tg OAE (câu b) => góc OAD = góc OAE
Mà tia OA nằm giữa 2 góc này
=> OA là tia pg của góc BAC
d, Xét tg ABC cân tại A có: \(\widehat{B}=\widehat{C}=\frac{180^o-\widehat{A}}{2}\) (3)
Lại có AD=AE (tg ABD = tg ACE) => tg ADE cân tại A => \(\widehat{ADE}=\widehat{AED}=\frac{180-\widehat{A}}{2}\) (4)
Từ (3),(4) => \(\widehat{B}=\widehat{C}=\widehat{ADE}=\widehat{AED}\) hay góc B = góc AED
mà 2 góc này ở vị trí đồng vị
=>DE//BC