
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


các bạn giúp mình nhé sáng thứ tư mình nộp bài rồi cảm ơn

a: Xét ΔCAB có CA^2+CB^2=AB^2
nên ΔCAB vuông tại C
Xét ΔCAB vuông tại C có CH là đường cao
nên CH*AB=CA*CB
=>CH*25=15*20=300
=>CH=12(cm)
b: góc BCD+góc ACD=90 độ
góc BDC+góc HCD=90 độ
mà góc ACD=góc HCD
nên góc BCD=góc BDC
=>ΔBDC cân tại B
c: BC^2+BD^2+CD^2
=BC^2+BC^2+CD^2
=2BC^2+CD^2
=2(BH^2+HC^2)+CH^2+HD^2
=2BH^2+3CH^2+DH^2

Trong △ABC, ta có: AD là đường phân giác của (BAC)
Suy ra: (tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên
Suy ra: (tính chất tỉ lệ thức)
Suy ra:
Trong △ABC, ta có: AD là đường phân giác của (BAC)
Suy ra: (tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên
Suy ra: (tính chất tỉ lệ thức)
Suy ra:

a: BC=13cm
\(AB=3\sqrt{13}\left(cm\right)\)
\(AC=2\sqrt{13}\left(cm\right)\)

a: Ta có: ΔBKC vuông tại K
mà KH là trung tuyến
nên KH=BH
=>ΔHBK cân tại H
b: góc BAH=90 độ-góc ABC
góc IAK=90 độ-góc ACB
mà góc ABC=góc ACB
nên góc BAH=góc IAK
c: Gọi G là trung điểm của AI
góc GKH=góc GKI+góc HKI
=góc GIK+góc HBI
=góc BIH+góc HBI=90 độ
=>HK là tiếp tuyến của (G)
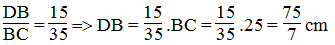
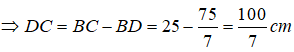
Vì CH là đường cao nên CH vuông BC
\(BC^2=BH^2+CH^2\)(1)
\(AC^2=AH^2+HC^2\)(2)
Lấy (1) - (2) ta được :
\(BC^2-AC^2=BH^2-AH^2\)
mà tam giác ABC cân nên CH là đường cao hay CH là trung tuyến
\(\Rightarrow BC^2-AC^2=0\Rightarrow BC^2=AC^2\)
lại có : \(AC^2=AB^2\Rightarrow BC^2=AB^2=AB.AB=2BH.AB\)( đpcm )
https://www.googleadservices.com/pagead/aclk?sa=L&ai=C1xTO4p68YNz8KZW9qAHPy5LIDMmr6qNg0NOfg5kLwI23ARABINzsuC5gwQWgAZ7U484DyAEBqQINxZei7dzHPagDAcgDwwSqBMsBT9BTpRx9neIyrGO0O1963KuNmKBbxmGUtm-UAFO5AJXWfGhNypiODjI2tMBBsAxtTOKP603Lj3je5QQRx3ovhk8kcnnZ93EdoUFKtIfQ7jNaTP1DRpyH3y7auZXCUyvspX9qBZEFNAcV6T0_zEqR9ahsF-pKVxzj0G4oSE7mhCvi1sG4B097ERVJq_aNPyK_D7SmVwoVrcjkAfcWeX7qSdiA0lC5ml0043ZOXX-lVQaHdEX1us_fzL7ZFFc6436j-L8Q9e9-AVNaNvzABKml1oj1AqAGUYAHyqucMagHipyxAqgH1ckbqAfw2RuoB_LZG6gHjs4bqAeT2BuoB7oGqAfulrECqAemvhuoB-zVG6gH89EbqAfs1RuoB5bYG9gHAdIIBwiAYRABGB-xCelDaA8avH1pgAoBmAsByAsBuAwB2BMN0BUBmBYBgBcB&ae=1&num=1&cid=CAASEuRosVrTt0fMF44rjoYpSKVXWQ&sig=AOD64_3I3-_NQIpH8DjLwEZVT3ytqgp_Iw&client=ca-pub-2208223212947843&nb=1&adurl=https://hoidap247.com/%3Fgclid%3DEAIaIQobChMI3PWZ--GC8QIVlR4qCh3PpQTJEAEYASAAEgJrHfD_BwE