Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

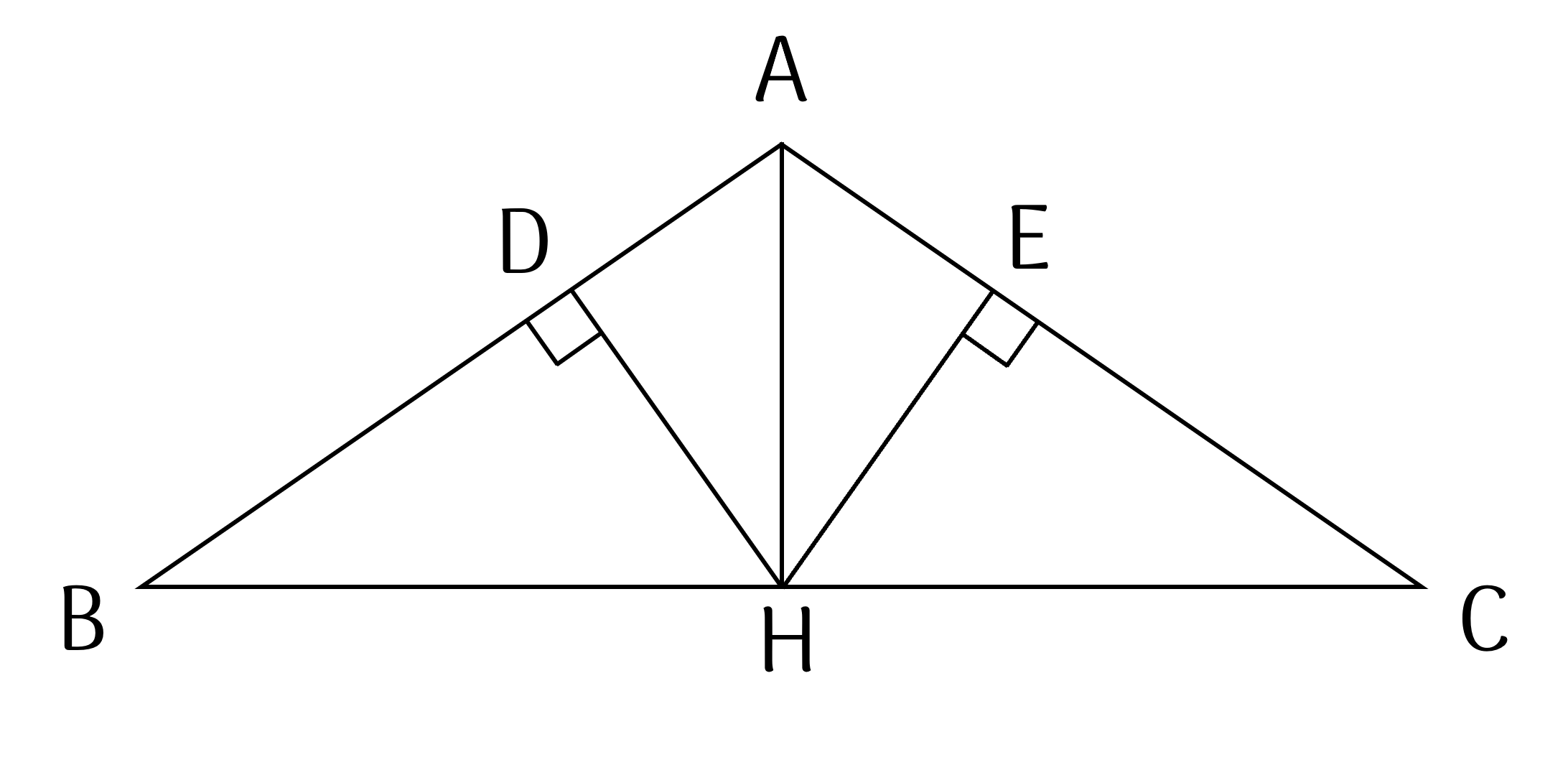
a) Xét hai tam giác vuông $AHB$ và $AHC$ có:
$AH$ là cạnh chung;
$AB = AC$ (gt);
Suy ra $\Delta AHB=\Delta AHC$ (cạnh huyền - cạnh góc vuông)
Suy ra $HB = HC$ (Hai cạnh tương ứng)
$\widehat{BAH} = \widehat{CAH}$ (hai góc tương ứng).
b) Xét hai tam giác vuông $ADH$ và $AEH$ có:
$AH$ là cạnh chung;
$\widehat{BAH} = \widehat{CAH}$ (cmt);
Suy ra $\Delta ADH=\Delta AEH$ (cạnh huyền - góc nhọn).
Suy ra $HD = HE$ (Hai cạnh tương ứng) nên $\Delta HDE$ cân tại $H$.

XÉT TAM GIÁC AHB VÀ TAM GIÁC AHC CÓ
AB=AC(GT)
AH CHUNG
GÓC AHB = GÓC AHC
=>TAM GIÁC AHB=TAM GIÁC AHC (CGC)
C,XÉT TAM GIÁC AHE VÀ TAM GIÁC AFH CÓ
AH CHUNG
GÓC AEH=GÓC AFH =90*
A1=A2
=>TAM GIÁC AHE=TAM GIÁC AFH (GCG)
=>HE=HF (CẠNH TƯƠNG ỨNG)

a, Xét △BAH vuông tại H và △CAH vuông tại H
Có: AB = AC (△ABC cân tại A)
AH là cạnh chung
=> △BAH = △CAH (ch-cgv)
=> BAH = CAH (2 góc tương ứng)
b, Ta có: BH + HC = BC => BH + HC = 8
Mà BH = HC (△BAH = △CAH)
=> BH = HC = 8 : 2 = 4 (cm)
Xét △AHC vuông tại H
Có: AC2 = AH2 + HC2
=> AC2 = 32 + 42
=> AC2 = 9 + 16
=> AC2 = 25
=> AC = 5 (cm)
c, Xét △EAH vuông tại E và △DAH vuông tại D
Có: AH là cạnh chung
EAH = DAH (cmt)
=> △EAH = △DAH (ch-gn)
=> AE = AD (2 cạnh tương ứng)
d, Xét △AED có: AE = AD (cmt) => △AED cân tại A
=> AED = (180o - EAD) : 2 (1)
Vì △ABC cân tại A => ABC = (180o - BAC) : 2 (2)
Từ (1) và (2) => AED = ABC
Mà 2 góc này nằm ở vị trí đồng vị
=> ED // BC (dhnb)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC và \(\widehat{BAH}=\widehat{CAH}\)
b: Ta có: HB=HC
H nằm giữa B và C
Do đó: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=4\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-4^2=9\)
=>\(AH=\sqrt{9}=3\left(cm\right)\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là tia phân giác của góc BAC
=>HB=HC và góc BAH=góc CAH
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: AD=AE và HD=HE
hay ΔHED cân tại H

a, Xét hai tam giác vuông ABH và tam giác vuông ACH có :
góc AHB = góc AHC = 90độ
AB = AC ( vì tam giác ABC cân tại A )
cạnh AH chung
Do đó : tam giác ABH = tam giác ACH ( cạnh huyền - cạnh góc vuông )
=> HB = HC ( cạnh tương ứng )
và góc BAH = góc CAH ( góc tương ứng )
b,Xét tam giác AHE và tam giác AHF có :
góc AEH = góc AFH = 90độ
cạnh AH chung
góc HAE = góc HAF ( theo câu a )
Do đó ; tam giác AHE = tam giác AHF ( cạnh huyền - góc nhọn )
=> AE = AF ( cạnh tương ứng )
=> tam giác AEF cân tại A
=> góc AEF = góc AFE = \(\frac{180^0-\widehat{A}}{2}\) ( 1 )
Vì tam giác ABC là tam giác cân nên :
góc ABC = góc ACB = \(\frac{180^0-\widehat{A}}{2}\) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra : góc AEF = góc AFE = góc ABC = góc ACB
mà góc AEF = góc ABC và ở vị trí đồng vị
=> EF // BC .
Học tốt
Bằng câu trả lời