Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

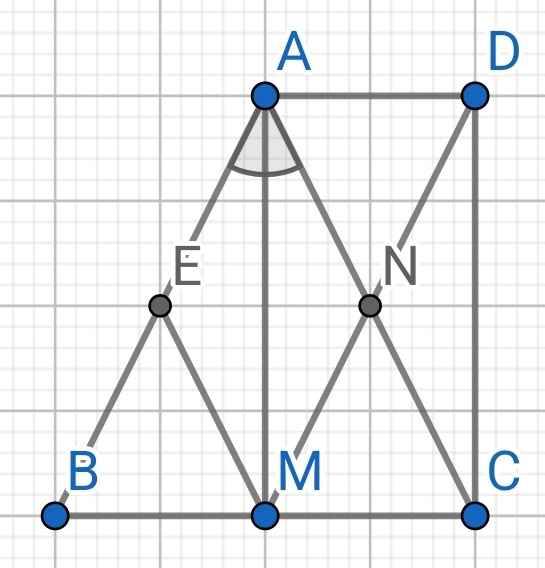 a) Do MN // AB (gt)
a) Do MN // AB (gt)
⇒ MN // AE
Do ME // AC (gt)
⇒ ME // AN
Do AM là tia phân giác của ∠BAC (gt)
⇒ AM là tia phân giác của ∠EAN
Xét tứ giác AEMN có:
MN // AE (cmt)
ME // AN (cmt)
⇒ AEMN là hình bình hành
Mà AM là tia phân giác của ∠EAN (cmt)
⇒ AEMN là hình thoi
b) Do D là điểm đối xứng của M qua N (gt)
⇒ N là trung điểm của DM
∆ABC cân tại A có AM là tia phân giác của ∠BAC (gt)
⇒ AM cũng là đường trung trực của ∆ABC
⇒ M là trung điểm của BC
∆ABC có:
M là trung điểm của BC (cmt)
MN // AB (gt)
⇒ N là trung điểm của AC
Tứ giác ADCM có:
N là trung điểm của DM (cmt)
N là trung điểm của AC (cmt)
⇒ ADCM là hình bình hành
⇒ AD // CM
⇒ AD // BM
Do MN // AB (gt)
⇒ MD // AB
Tứ giác ADMB có:
MD // AB (cmt)
AD // BM (cmt)
⇒ ADMB là hình bình hành

bài 1 sai đề rồi bạn. Nếu BEMD là ht cân thật thì \(\widehat{ABC}=\widehat{MDB}\)mà \(\widehat{MDB}=\widehat{ACB}\)(đồng vị) => \(\widehat{ABC}=\widehat{ACB}\)=> tam giác ABC cân( trái với đề bài)

1. ta có AD = BC (gt)
mà DH = BF (gt)
=> AH =FC
xét ▲AHE và ▲FCG, có:
AE = CG (gt)
góc A = góc C (gt)
AH = FC (cmt)
=>▲AHE = ▲FCG (c.g.c)
=>HE = FG (2 cạnh t/ứ)
cmtt : HG = EF
Vậy EFGH là hbh (đpcm)