Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác EAB và tam giác DAC có:
AB = AC (gt)
AD = AE (gt)
BE = CD (BE = BD + DE = DE + EC = CD)
=> Tam giác EAB = Tam giác DAC (c.c.c)
M là trung điểm của BC
=> AM là đường trung tuyến của tam giác ABC cân tại A (AB = AC)
=> AM là đường cao của tam giác ABC
hay AM _I_ BC
mà D, E thuộc BC
=> AM _I_ DE
hay AM là đường cao của tam giác ADE cân tại A (AD = AE)
=> AM là tia phân giác của DAE
Tam giác ADE cân tại A (AD = AE)
mà DAE = 600
=> Tam giác ADE là tam giác đều
=> ADE = AED = 600
đây là cách làm của lớp 9 rồi,toán lớp 7 chưa học đường cao của tam giác

a. Xét tam giác EBA và tam giác DCA
AB=AC
AE=AD
BE=DC
=> tam giác EBA= tam giác DCA(ccc)
b. Theo câu a, tam giác EBA= tam giác DCA(ccc)=> AE=AD; AEB=ADC
Xét tam giác DAM và tam giác EAM có
AD=AE
ADM=AEM
DM=EM
=> tam giác DAM=tam giác EAM(cgc)
=> DAM=EAM => AM là phân giác DAE
c. Nếu DAE=60*
Xét tam giác DAE có AD=AE và DAE=60*=> tam giác DAE là tam giác đều
=> ADE=AED=DAE=60*

a) Tam giác ABC có AB = AC nên tam giác ABC cân tại A
\(\Delta ABE\)= \(\Delta ACD\) ( cgc ) ( AB = AC (gt) ; \(\widehat{B}\) =\(\widehat{C}\) ( tam giác ABC cân tại A) ; BE = CD = \(\frac{2}{3}\) BC )
Do đó \(\widehat{BAE}\) = \(\widehat{DAC}\) => tam giác DAE cân tại A
b) tam giác ABC cân tại A có AM là đường trung tuyến => AM là đường cao của tam giác ABC .
Tam giác DAE cân tại A có AM là đường cao ứng với cạnh DE => AM là đường phân giác của tam giác DAE => AM là tia phân giác của \(\widehat{DAE}\)
c) Tam giác DAE cân tại A có \(\widehat{DAE}\) = 600 => Tam giác DAE là tam giác đều => mỗi góc trong tam giác DAE đều là 600

Ta có :
\(BD=DE=EC\)
\(\Rightarrow BD+DE=EC+DE\)
\(\Rightarrow BE=DC\)
=> Ta c/m được \(\Delta EAB=\Delta DAC\left(C.g.c\right)\)
\(\Rightarrow\widehat{EAB}=\widehat{DAC}\)
=> AD = AE
b)
Vì M là trung điểm của BC
\(\Rightarrow BM=CM\)
\(\Rightarrow BD+DM=ME+EC\)
Mà BD = EC
\(\Rightarrow DM=EM\)
=> \(\Rightarrow\Delta DAM=\Delta EAM\left(c.c.c\right)\)
\(\Rightarrow\widehat{DAM}=\widehat{EAM}\)
=> AM là tia phân giác của góc DAE
c)
Nếu \(\widehat{A}=60^0\)
Mà AD=AE
=> tam giác ADE đều
=> Các góc còn lại cũng bằng 600
Giải:
a) Ta có: \(BD=DE=EC\left(gt\right)\)
\(\Rightarrow BD+DE=EC+DE\)
\(\Rightarrow BE=CD\) (*)
Xét \(\Delta EAB,\Delta DAC\) có:
\(BE=CE\) ( theo (*) )
\(\widehat{B}=\widehat{C}\) ( do \(\Delta ABC\) cân tại A vì AB = AC )
\(AB=AC\left(gt\right)\)
\(\Rightarrow\Delta EAB=\Delta DAC\left(c-g-c\right)\)
\(\Rightarrow\widehat{EAB}=\widehat{DAC}\) ( góc t/ứng )
b) Vì \(\Delta EAB=\Delta DAC\)
\(\Rightarrow AD=AE\) ( cạnh t/ứng )
\(\Rightarrow\Delta DAE\) cân tại A
\(\Rightarrow\widehat{ADE}=\widehat{AED}\) (**)
Xét \(\Delta DAM,\Delta EAM\) có:
\(MD=ME\left(=\frac{1}{2}DE\right)\)
\(\widehat{ADE}=\widehat{AED}\) ( theo (**) )
AM: cạnh chung
\(\Rightarrow\Delta DAM=\Delta EAM\left(c-g-c\right)\)
\(\Rightarrow\widehat{DAM}=\widehat{EAM}\) ( góc t/ứng )
\(\Rightarrow\)AM là tia phân giác của \(\widehat{DAE}\)
c) Trong \(\Delta AED\) cân tại A có \(\widehat{DEA}=60^o\)
\(\Rightarrow\Delta AED\) là một tam giác đều
Vậy...
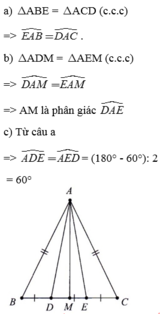
Cho \(\Delta ABC\)cân tại A,hai điểm D và E thuộc cạnh BC sao cho BD = DE = EC.Biết AD = AE
a) Chứng minh \(\widehat{EAB}=\widehat{DAC}\)(sửa câu a nhé bạn,thế chỗ AD = AE vào tiêu đề)
a) Xét \(\Delta\)AEB và \(\Delta\)ADE có :
AB = AE (gt)
EB = ED (gt)
AE = AD(gt)
=> \(\Delta AEB=\Delta ADE\left(c-c-c\right)\)
=> \(\widehat{EAB}=\widehat{DAC}\)(hai góc tương ứng)
b)
Ta có : BM = BD + DM
CM = CE + EM
Mà M là trung điểm của BC(gt) nên BM = CM,do đó : MD = ME
Mặt khác AD = AE (gt) , cạnh AM chung vì thế \(\Delta AMD=\Delta AME\left(c-c-c\right)\)
=> \(\widehat{MAD}=\widehat{MAE}\)(hai góc tương ứng)
Vậy AM là tia phân giác của góc DAE.
c) \(\Delta ADE\)có AD = AE
=> \(\Delta ADE\)cân tại A
=> \(\widehat{ADE}=\widehat{AED}\)
Xét \(\Delta ADE\)ta có :
\(\widehat{ADE}+\widehat{AED}+\widehat{DAE}=180^0\)(định lí tổng 3 góc trong 1 tam giác)
=> \(2\widehat{ADE}+\widehat{DAE}=180^0\)
=> \(2\widehat{ADE}+60^0=180^0\)
=> \(2\widehat{ADE}=120^0\)
=> \(\widehat{ADE}=60^0\)
Mà \(\widehat{ADE}=\widehat{AED}\)(cmt)
=> \(\widehat{ADE}=\widehat{AED}=60^0\)