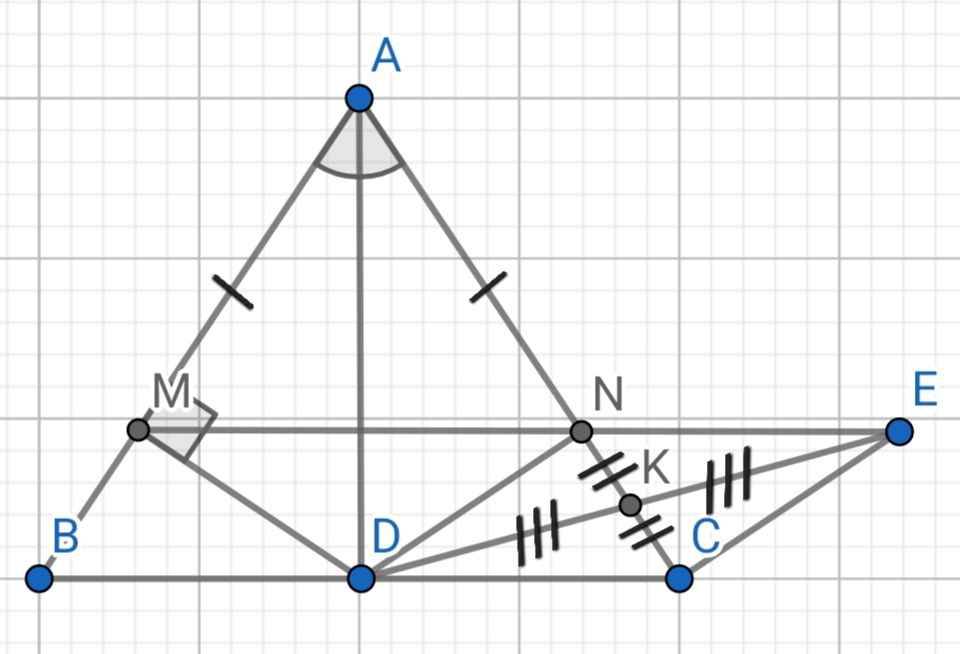a) Do AD là tia phân giác của ∠BAC (gt)

⇒ ∠BAD = ∠CAD

Do ∆ABC cân tại A

⇒ AB = AC

Xét ∆ABD và ∆ACD có:

AB = AC (cmt)

∠BAD = ∠CAD (cmt)

AD là cạnh chung

⇒ ∆ABD = ∆ACD (c-g-c)

⇒ BD = CD

⇒ D là trung điểm của BC (1)

Do ∆ABD = ∆ACD (cmt)

⇒ ∠ADB = ∠ADC (hai góc tương ứng)

Mà ∠ADB + ∠ADC = 180⁰ (kề bù)

⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰

⇒ AD ⊥ BC (2)

Từ (1) và (2) ⇒ AD là đường trung trực của BC

b) Sửa đề: Chứng minh ∆ADM = ∆ADN

Do ∠BAD = ∠CAD (cmt)

⇒ ∠MAD = ∠NAD

Xét ∆ADM và ∆ADN có:

AD là cạnh chung

∠MAD = ∠NAD (cmt)

AM = AN (gt)

⇒ ∆ADM = ∆ADN (c-g-c)

⇒ ∠AMD = ∠AND = 90⁰ (hai góc tương ứng)

⇒ DN ⊥ AN

⇒ DN ⊥ AC

d) Do K là trung điểm của CN (gt)

⇒ CK = KN

Xét ∆DKC và ∆EKN có:

CK = KN (cmt)

∠DKC = ∠EKN (đối đỉnh)

KD = KE (gt)

⇒ ∆DKC = ∆EKN (c-g-c)

⇒ ∠KDC = ∠KEN (hai góc tương ứng)

Mà ∠KDC và ∠KEN là hai góc so le trong

⇒ EN // CD

⇒ EN // BC (3)

∆AMN có:

AM = AN (gt)

⇒ ∆AMN cân tại A

⇒ ∠AMN = (180⁰ - ∠MAN) : 2

= (180⁰ - ∠BAC) : 2 (4)

∆ABC cân tại A (gt)

⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (5)

Từ (4) và (5) ⇒ ∠AMN = ∠ABC

Mà ∠AMN và ∠ABC là hai góc đồng vị

⇒ MN // BC (6)

Từ (3) và (6) kết hợp với tiên đề Euclide ⇒ M, N, E thẳng hàng

Bạn tự vẽ hình nha 

a) Cét 2 tam giác ABD VÀ ACD ta có : 

AB = AC ( vì tam giác ABC cân ) 

góc A1 = A2 ( vì AD là tia pg của góc BAC ) 

AD là cạnh chung 

= > tam giác ABD = ACD ( c.g.c ) 

b) Vì tg ABD = ACD ( cmt ) 

=> góc D1 = D2 ( 2 góc tương ứng ) 

mà D1 và D2 là 2 góc kề bù 

= > góc D1 + D2 = 180 độ 

mà D1 = D2 

=> D1= D2= 180 độ : 2 = 90 độ 

=>AD vuông góc với BC

c) Vì MD song song với AC 

=> D1 = góc C ( 2 góc đồng vị ) 

mà góc B=C 

=> B = D1 

=> Tg MBD cân tại M 

=> MB = MD 

Câu d bạn tự làm nha 

Bạn tự vẽ hình nha 
a) Cét 2 tam giác ABD VÀ ACD ta có : 
AB = AC ( vì tam giác ABC cân ) 
góc A1 = A2 ( vì AD là tia pg của góc BAC ) 
AD là cạnh chung 
= > tam giác ABD = ACD ( c.g.c ) 
b) Vì tg ABD = ACD ( cmt ) 
=> góc D1 = D2 ( 2 góc tương ứng ) 
mà D1 và D2 là 2 góc kề bù 
= > góc D1 + D2 = 180 độ 
mà D1 = D2 
=> D1= D2= 180 độ : 2 = 90 độ 
=>AD vuông góc với BC
c) Vì MD song song với AC 
=> D1 = góc C ( 2 góc đồng vị ) 
mà góc B=C 
=> B = D1 
=> Tg MBD cân tại M 
=> MB = MD 
Câu d bạn tự làm nha 

 xét∆ABD và∆ACD có:
BD=CD
AB=AC
Chung AD
=) ∆ABD=∆ACD( c-g-c )
b)do AB=AC =) ∆ABC cân tai A .                      
Lại có: BD=CD=)AD là trung tuyến∆ABC .     
Suy ra AD là phân giác góc BAC
c) do trong∆ cân thì đường trung tuyến vừa là phân giác vừa là đường cao vừa là trung trực nên AD vuông góc với BC

=>AD vuông góc với BC
mà BC//d
=>  AD vuông góc với d

đáng ra phỉa là c-c-c chứ

1/

a/ Ta có AB < BC (5cm < 6cm)

=> \(\widehat{ACB}< \widehat{A}\)(quan hệ giữa góc và cạnh đối diện trong tam giác)

Mà \(\widehat{ACB}=\widehat{ABC}\)(\(\Delta ABC\)cân tại A)

=> \(\widehat{ABC}< \widehat{A}\)

b/ \(\Delta ADB\)và \(\Delta ADC\)có: AB = AC (\(\Delta ABC\)cân tại A)

\(\widehat{BAD}=\widehat{DAC}\)(AD là tia phân giác \(\widehat{BAC}\))

Cạnh AD chung

=> \(\Delta ADB\)= \(\Delta ADC\)(c. g. c) (đpcm)

c/ Ta có \(\Delta ABC\)cân tại A

=> Đường cao AD cũng là đường trung tuyến của \(\Delta ABC\)

và G là giao điểm của hai đường trung tuyến AD và BE của \(\Delta ABC\)

=> CF là đường trung tuyến thứ ba của \(\Delta ABC\)

=> F là trung điểm AB (đpcm)

d/ Ta có G là giao điểm của ba đường trung tuyến AD, BE và CF của \(\Delta ABC\)

=> G là trọng tâm \(\Delta ABC\)

và D là trung điểm BC (vì AD là đường trung tuyến của \(\Delta ABC\))

=> \(BD=DC=\frac{BC}{2}=\frac{6}{2}=3\)(cm)

Áp dụng định lý Pitago vào \(\Delta ADB\)vuông tại D, ta có: AD = 4cm (tự tính)

=> \(AG=\frac{2}{3}AD=\frac{2}{3}.4=\frac{8}{3}\)(cm)

Áp dụng định lý Pitago vào \(\Delta ADC\)vuông tại D, ta có:

\(BG=\sqrt{BD^2+GD^2}\)

=> \(BG=\sqrt{3^2+\left(\frac{8}{3}\right)^2}\)

=> \(BG=\sqrt{9+\frac{64}{9}}\)

=> \(BG=\sqrt{\frac{145}{9}}\)

=> BG \(\approx\)4, 01 (cm)

â)xét tam giác abd và acd có 

ab=ac(abc là tam giác cân )

ad chung

góc a1=a2(ad là tia phân giác góc a)

=>tam giác abd=acd(trường hợp cạnh-góc -cạnh)

b)vì tam giác abc=acd(câu a)=>bd=cd=>ad là trung tuyến cạnh bc

mà cf là đuong trung tuyển cạnh ba=>ad và cf cùng đi qua một điểm

=> g là trọng tâm

câu c mình vẫn chưa nghĩ ra được .xin lỗi nha

c) H là trung điểm của CD \(\Rightarrow\)DH=HC

mà EH vuông góc vs DC \(\Rightarrow\) EH là đường cao

\(\Rightarrow\)EH là đường trung trực của CD \(\Rightarrow\)ED=EC \(\Rightarrow\)tam giác DEC cân  tại E

d) tam giác GBC cân tại G ( CM tương tự như trên )

\(\Rightarrow\)  góc GBC =GCB

mà \(\widehat{B}=\widehat{C}\)(tam giác ABC cân tại A) 

\(\widehat{GBD}+\widehat{ABE}=\widehat{B}\) ;  \(\widehat{GCB}+\widehat{ACF}=\widehat{C}\)

\(\Rightarrow\) GÓC ABE = ACF

TAM GIÁC ABE = TAM GIÁC ACF  (G.C.G)

\(\Rightarrow\) AE=AF

MÀ AF=1/2AB ( CF là đường trung tuyến ) ; AB=AC (tam giác ABC cân tại A )

\(\Rightarrow\) AE = 1/2 AC \(\Rightarrow\) E LÀ TRUNG ĐIỂM CỦA AC

\(\Rightarrow\) BE LÀ ĐƯỜNG TRUNG TUYẾN

mà G là trọng tâm của tam giác ABC

\(\Rightarrow\)BE đi qua G \(\Rightarrow\)3 điểm B,E,G thẳng hàng

a, Vì tam giác ABC cân tại A 

AB = AC ( tính chất )

Xét tam giác ABH và tam giác ACD có 

        AB = AC

        AD chung

        BD=DC

suy ra 2 tam giác bàng nhau ( c.c.c) đúng ko ae