Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD và ΔACD có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔABD=ΔACD
=>BD=CD và góc ADB=góc ADC=180/2=90 độ
=>AD vuông góc bC
b: BD=CD=18/2=9cm
AD=căn 15^2-9^2=12cm
c: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
góc KBC=góc HCB
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>ΔIBC cân tại I

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB chung
=>ΔAHB=ΔAKC
=>AH=AK
b:
Xét ΔABC có
BH,CK là đường cao
BH cắt CK tại I
=>I là trực tâm
=>AI vuông góc BC tại M
Xét ΔKBC vuông tạiK và ΔHCB vuông tại H có
BC chung
KC=HB
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác
c: Xet ΔBAC có AK/AB=AH/AC
nên KH//BC

xét tam giác ABC cân tại A
=> AB=AC(t/c tam giác cân)
=>^ABC=^ACB(t/c tam giác cân)
xét tam giác BAH và tam giác CAK
^A chung
AB=AC(cmt)
^AHB=^AKC
=> tam giác BAH = tam giác CAK(gcg)
=>BH=CK(2 cạnh tương ứng)
=>CH=BK (2 cạnh tương ứng)
b) bạn kiểm tra lại đề bài câu b nhé ! mik chưa thấy dữ kiện nào nói về điểm D cả
c) Ta có : AB=BK+AK
AC=CH+AH
mà AB=AC(cmt);CH=BK(cmt)
=> AK=AH
xét tam giác KAO và tam giác HAO
AK=AH(cmt)
^AKO=^AHO=90o
AO-cạnh chung
=> tam giác KAO = tam giác HAO (ch-cgv)
=>^KAO=^HAO(2 góc tương ứng)
=>^BAI=^CAI
xét tam giác BAI và tam giác CAI
AB=AC(cmt)
^BAI=^CAI(cmt)
AI-cạnh chung
=> tam giác BAI = tam giác CAI
=>^AIB=^AIC ( 2 góc tương ứng)
mà ^AIB+^AIC=180o(kề bù)
=> ^AIB=^AIC=90o
=>AI vuông góc BC
bài 2 bạn tham khảo tại link này
https://h o c 2 4.vn/hoi-dap/question/494804.html
nhớ viết liền từ h o c 2 4 nha! vì olm ko cho viết

a: Xet ΔAHB vuông tại H và ΔAKC vuông tại K có
góc BAH chung
AB=AC
=>ΔAHB=ΔAKC
=>AH=AK
=>ΔAHK cân tại A
b: góc ABH+góc HBC=góc ABC
gócACK+góc ICB=góc ACB
mà góc ABC=góc ACB; góc ABH=góc ACK
nên góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác của góc BIC

a: Ta có: \(\widehat{ABC}+\widehat{ABM}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
=>AM=AN
=>ΔAMN cân tại A
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)(ΔABM=ΔACN)
Do đó: ΔAHB=ΔAKC
=>HB=KC và AH=AK
c: Sửa đề: HB cắt KC tại O
Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
BM=CN
HB=KC
Do đó: ΔHBM=ΔKCN
=>\(\widehat{HBM}=\widehat{KCN}\)
Ta có: \(\widehat{HBM}=\widehat{KCN}\)
\(\widehat{OBC}=\widehat{HBM}\)(hai góc đối đỉnh)
\(\widehat{OCB}=\widehat{KCN}\)(hai góc đối đỉnh)
Do đó: \(\widehat{OBC}=\widehat{OCB}\)
=>ΔOBC cân tại O
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(1)
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC
Xét ΔABO và ΔACO có
AO chung
AB=AC
BO=CO
Do đó: ΔABO=ΔACO
=>\(\widehat{BAO}=\widehat{CAO}\)
=>AO là phân giác của góc BAC

a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
góc A chung
=>ΔABH=ΔACK
b: góc KBC+góc ICB=90 độ
góc IBC+góc HCB=90 độ
mà góc KBC=góc HCB
nên góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác của góc BIC
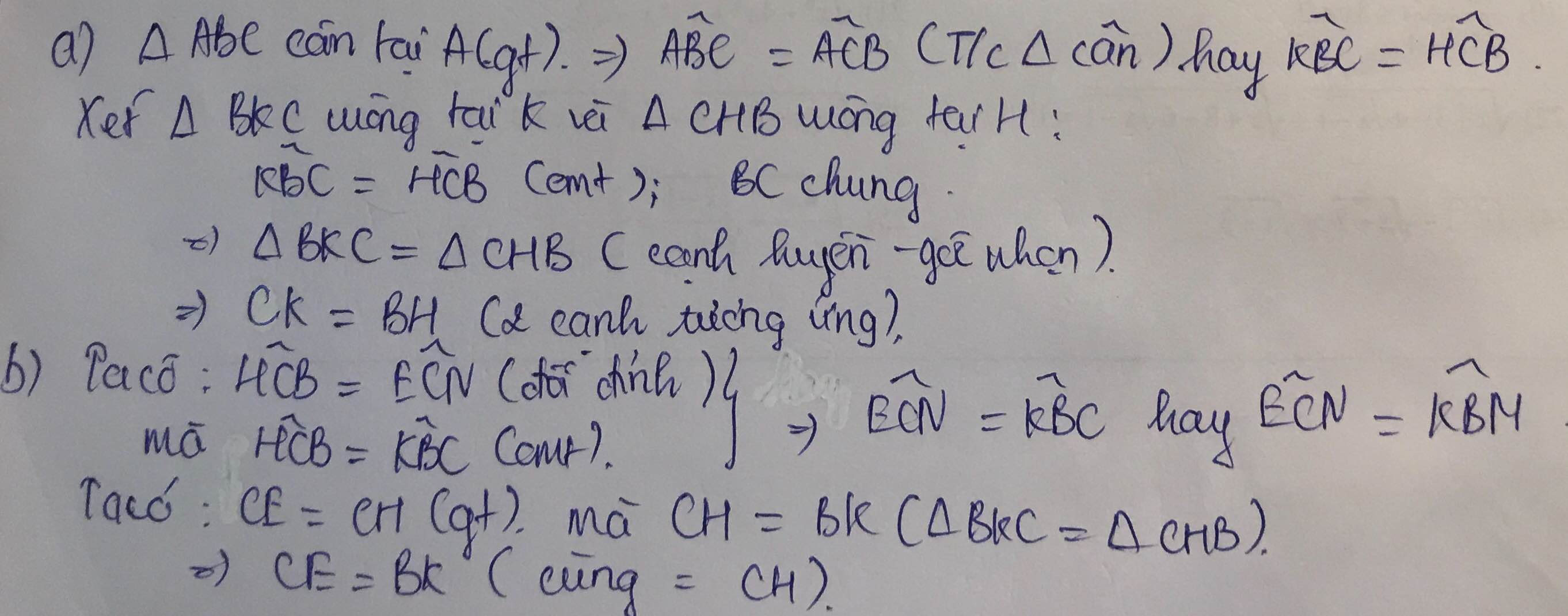

 hãy cho mk 1 L-I-K-E
hãy cho mk 1 L-I-K-E