Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề bài “Dây quấn ống trụ tròn” như sau:
"A string is wound symmetrically around a circular rod. The string goes exactly 4 times around the rod. The circumference of the rod is 4 cm. and its length is 12 cm. Find the length of the string? Show all your work".
Tạm dịch là:
“Một sợi dây được quấn đối xứng 4 vòng quanh một ống trụ tròn đều. Ống trụ có chu vi 4 cm và độ dài là 12 cm.
Do chu vi ống trụ là 4 cm nên khi "trải phẳng" ống trụ, ta sẽ được một hình chữ nhật có kích thước 4x12 (cm).
Sợi dây duỗi thẳng sẽ trở thành 4 đường chéo của 4 hình chữ nhật có kích thước 3x4 (cm).
Áp dụng định lý Pi-ta-go, ta có chiều dài mỗi đường chéo (hay mỗi đoạn dây) sẽ là √3² + 4² = 5 (cm).
Do mỗi đường chéo có kích thước bằng nhau nên tổng chiều dài sợi dây là 5x 4= 20 (cm).
Đáp số; 20 cm
Áp dụng định lý Pi-ta-go, ta có chiều dài mỗi đường chéo (hay mỗi đoạn dây) sẽ là √3² + 4² = 5 (cm).
Do mỗi đường chéo có kích thước bằng nhau nên tổng chiều dài sợi dây là 5x 4= 20 (cm).
Đáp số; 20 cm

a) Ta có : Góc MDB = góc CME (gt) ; Góc B = góc C (tam giác ABC cân tại A)
=> \(\Delta DBM~\Delta MCE\left(g.g\right)\) \(\Rightarrow\frac{BM}{CE}=\frac{BD}{MC}\) hay \(\frac{BM}{CE}=\frac{BD}{BM}\) ( M là trung điểm BC)
\(\Rightarrow BM^2=BD.CE\)
b) Ta có : Góc BMD = góc MEC (tam giác DBM và MCE đồng dạng)
Mà BME là góc ngoài tam giác MEC => góc BMD + góc DME = góc MEC + góc MCE = góc BMD + góc MCE
=> Góc DME = góc MCE = góc MBA (1)
Từ \(\Delta DBM~\Delta MCE\left(g.g\right)\) \(\Rightarrow\frac{DM}{ME}=\frac{BM}{CE}\) hay \(\frac{DM}{ME}=\frac{MC}{CE}\) (2)
Từ (1) và (2) suy ra \(\Delta DME~\Delta MCE\left(c.g.c\right)\) mà \(\Delta DBM~\Delta MCE\left(g.g\right)\) \(\Rightarrow\Delta DBM~\Delta DME\)
Vậy ta có điều phải chứng minh.

a, ^BOD + ^OBD = 120 = ^BOD + ^EOC (vì ^DOE = 60)
=> ^BDO = ^EOC
=> ∆BDO đồng dạng ∆COE
=> BD/BO = CO/CE
<=> BD.CE = BC²/4
b, DO/OE = BD/CO
<=> BO/OE = BD/OD
=> ∆BOD đồng dạng ∆OED
=> ^BDO = ^ODE
=> OD là tia phân giác của góc BDE
c, kẻ OI,OK lần lượt vuông góc với AB,DE
AB tiếp xúc với (O;OI)
có ∆IOD = ∆KOD (cạnh huyền góc nhọn)
=> OI = OK
mà OK ┴ DE
=> (O) luôn tiếp xúc với DE
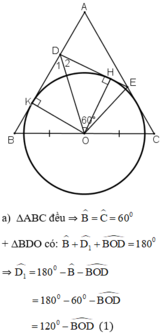
a) \(\Delta ABC\Rightarrow\widehat{B}=\widehat{C}=60^o\)
+) \(\Delta BDO\)có : \(\widehat{B}+\widehat{D_1}+\widehat{BOD}=180^o\)
\(\Rightarrow\widehat{D_1}=180^o-\widehat{B}-\widehat{BOD}\)
\(=180^o-60^o-\widehat{BOD}\)
\(=120^o-\widehat{BOD}\left(1\right)\)
Ta lại có :
\(\widehat{BOD}+\widehat{DOE}+\widehat{EOC}=\widehat{BOC}=180^o\)
\(\Rightarrow\widehat{EOC}=180^o-\widehat{DOE}-\widehat{BOD}\)
\(=180^o-60^o-\widehat{BOD}\)
\(=120^o-\widehat{BOD}\left(2\right)\)
Từ (1) và (2) , suy ra : \(\widehat{D_1}=\widehat{EOC}\)
\(\Delta BOD\)và \(\Delta EOC\)có :
\(\widehat{B}=\widehat{C}=60^o\)
\(\widehat{D_1}=\widehat{EOC}\left(cmt\right)\)
\(\Rightarrow\Delta BOD~\Delta EOC\)
\(\Rightarrow\frac{BO}{CE}=\frac{BD}{CO}\)
\(\Rightarrow BD.CE=BO.CO=\frac{BC^2}{4}\)
b) \(\Delta BOD~\Delta EOC\)
\(\Rightarrow\frac{OD}{EO}=\frac{BD}{CO}\)
mà CO = BO \(\Rightarrow\frac{OD}{EO}=\frac{BD}{BO}\)
\(\Delta BOD\)và \(\Delta OED\)có :
\(\widehat{B}=\widehat{O}\left(=60^o\right)\)
\(\frac{BD}{BO}=\frac{OD}{OE}\)
\(\Rightarrow\Delta BOD~\Delta OED\)
\(\Rightarrow\widehat{BDO}=\widehat{ODE}\)
=> OD là tia phân giác của góc BDE
c) Gọi đường tròn tâm O tiếp xúc với AB có bán kính R
Gọi H, K là chân đường vuông góc hạ từ O đến DE và AB
=> R = OK
O thuộc đường phân giác của \(\widehat{BDE}\)
=> OH = OK.
=> OH = R
=> DE tiếp xúc với ( O ; R ) (đpcm)

Lời giải
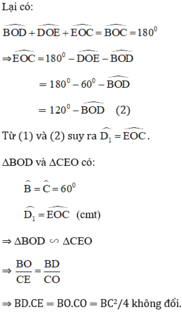
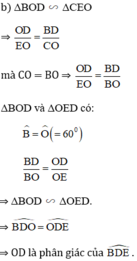
c) Gọi đường tròn tâm O tiếp xúc với AB có bán kính R.
Gọi H, K là chân đường vuông góc hạ từ O đến DE và AB.
⇒ R = OK.
O ∈ đường phân giác của 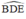
⇒ OH = OK.
⇒ OH = R
⇒ DE tiếp xúc với (O; R) (đpcm).

Lời giải

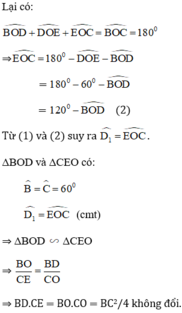
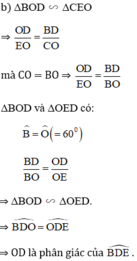
c) Gọi đường tròn tâm O tiếp xúc với AB có bán kính R.
Gọi H, K là chân đường vuông góc hạ từ O đến DE và AB.
⇒ R = OK.
O ∈ đường phân giác của 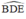
⇒ OH = OK.
⇒ OH = R
⇒ DE tiếp xúc với (O; R) (đpcm).

a, Ta có : \(\widehat{DMC}\) = \(\widehat{B} + \widehat{BDM}\)
Xét \(\bigtriangleup{DMB}\) và \(\bigtriangleup{MCE}\) , có :
\(\widehat{DME} = \widehat{B}\)
\(\widehat{BDM} = \widehat{EMC}\)
\(\Rightarrow\) \(\bigtriangleup{DMB}\) ~ \(\bigtriangleup{MCE}\) (g.g)
\(\Rightarrow\) \(\dfrac{DB}{BM} = \dfrac{MC}{EC} <=> BD.CE = BM . MC = a^2\) (đpcm)
b, Vì \(\bigtriangleup{DBM} \) \(\sim \) \(\bigtriangleup{MCE} <=> \dfrac{DM}{ME} = \dfrac{BD}{CM}\)
hay \(\dfrac{DM}{ME}= \dfrac{BD}{BM} \)
\(\Rightarrow\) \(\bigtriangleup{DME} \sim \bigtriangleup{DMB}\)
\(\Rightarrow\) \(\widehat{MDE} = \widehat{BDM} \)
\(\Rightarrow\) DM là tia phân giác của \(\widehat{BDE}\) (đpcm)
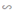 ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.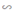 ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.