Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAEB vuông tại E và ΔADC vuông tại D có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔAEB=ΔADC

Vì tam giác ABC cân tại A (gt)
suy ra: góc ABC = góc ACB
hay góc EBC = góc DCB
Xét tam giác EBC và tam giác DCB có
góc BEC = góc CDB ( =90)
góc EBC = góc DCB (CMT)
BC chung
Suy ra tam giác EBC = tam giác DCB (ch-gn)
suy ra BE=CD (cctu)
Xét tg ABC có:
+ BD là đườg cao (BD vuông góc AC)
+ CE là đg cao (CE vuông góc AB)
Mà BD giao CE tại I (gt)
=> I là trực tâm
=> AI là đường cao
Xét tg ABC cân tai A có: AI là đường cao (cmt)
=> AI cũng là đường pg góc BAC ( Tc tg cân)

a)
Vì tam giác ABC cân tại A (gt)
suy ra: góc ABC = góc ACB
hay góc EBC = góc DCB
Xét tam giác EBC và tam giác DCB có
góc BEC = góc CDB ( =90)
góc EBC = góc DCB (CMT)
BC chung
Suy ra tam giác EBC = tam giác DCB (ch-gn)
suy ra BE=CD (cctu)
b) Xét tg ABC có:
+ BD là đườg cao (BD vuông góc AC)
+ CE là đg cao (CE vuông góc AB)
Mà BD giao CE tại I (gt)
=> I là trực tâm
=> AI là đường cao
Xét tg ABC cân tai A có: AI là đường cao (cmt)
=> AI cũng là đường pg góc BAC ( Tc tg cân)

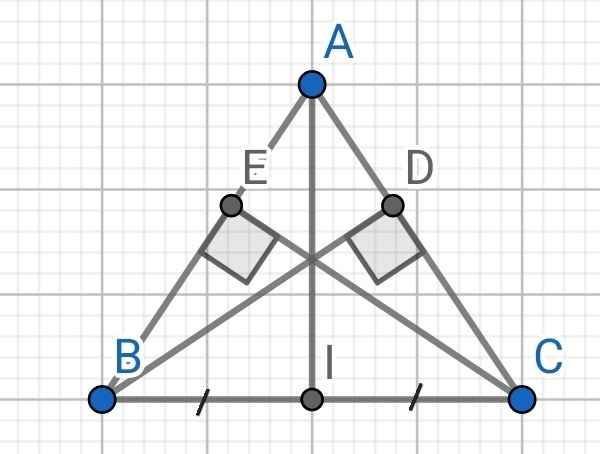 a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
AB = AC (do ∆ABC cân tại A)
∠A chung
⇒ ∆ABD = ∆ACE (cạnh huyền - góc nhọn)
b) Do I là trung điểm của BC (gt)
⇒ IB = IC
Xét ∆ABI và ∆ACI có:
AB = AC (cmt)
AI là cạnh chung
BI = CI (cmt)
⇒ ∆ABI = ∆ACI (c-c-c)
⇒ ∠BAI = ∠CAI (hai góc tương ứng)
⇒ AI là tia phân giác của ∠BAC
c) Do ∆ABI = ∆ACI (cmt)
⇒ ∠AIB = ∠AIC (hai góc tương ứng)
Mà ∠AIB + ∠AIC = 180⁰ (kề bù)
⇒ ∠AIB = ∠AIC = 180⁰ : 2 = 90⁰
⇒ AI ⊥ BC

a/ Xét tg vuông ADC và tg vuông AEB có
AB=AC
\(\widehat{A}\) chung
\(\Rightarrow\Delta ADC=\Delta AEB\) (Hai tg vuông có cạnh huyền và 1 góc nhọn tương ứng bằng nhau)
b/
Xét tg vuông ADI và tg vuông AEI có
AI chung
AD=AE (\(\Delta ADC=\Delta AEB\) )
\(\Rightarrow\Delta ADI=\Delta AEI\) (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{BAI}=\widehat{CAI}\) nên AI là phân giác của \(\widehat{BAC}\)