Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi $\widehat{A}, \widehat{B}, \widehat{C}$ là 3 góc trong tam giác $ABC$ và $\widehat{A_1}, \widehat{B_1}, \widehat{C_1}$ tương ứng là 3 góc ngoài 3 đỉnh.
Ta có:
$\widehat{A_1}+\widehat{B_1}+\widehat{C_1}=(180^0-\widehat{A})+(180^0-\widehat{B})+(180^0-\widehat{C})$
$=540^0-(\widehat{A}+\widehat{B}+\widehat{C})$
$=540^0-180^0=360^0$

a. B = 55 độ
C = 35
b. lỗi. phải là 360 độ
ông họ ngô
tôi họ đinh

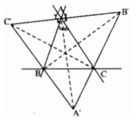
Ta có AA′⊥ AB′ vì chúng là hai tia phân giác của hai góc kề bù. Tương tự AA′⊥ AC′. Vì qua A chỉ có một đường vuông góc với AA' nên ba điểm B', A, C' thẳng hàng và AA′⊥ B′C′, hay A'A là một đường cao của tam giác A'B'C'. Hoàn toàn tương tự ta chứng minh được BB' và CC' là hai đường cao của tam giác A'B'C'.
Mặt khác theo cách chứng minh của bài 9.5 ta có AA', BB', CC' là ba tia phân giác của các góc A, B, C của tam giác ABC. Từ đó suy ra giao điểm của ba đường phân giác của tam giác ABC là trực tâm của tam giác A'B'C'.

Ta sử dụng tính chất: hai tia phân giác của hai góc kề bù thì vuông góc với nhau
+) BM; BI là 2 tia p/g của góc B trong và ngoài tam giác => BM | BI => góc MBI = 90o
CN và CI là 2 tia p/g của góc C trong và ngoài tam giác ABC => CN | CI => góc ICN = 90o
+) Xét tam giác MBC có: góc M + MCB + MBC = 180o => góc M + MCB + (MBI + IBC) = 180o
=> góc M + góc \(\frac{C}{2}\) + góc \(\frac{B}{2}\) + 90o = 180o => góc M + góc \(\frac{B+C}{2}\) = 90o => góc M = 90o - góc \(\frac{B+C}{2}\) = \(\frac{180^o-\left(B+C\right)}{2}=\frac{A}{2}\)
+) tương tự, ta có góc N = góc A/2
Vậy góc M = Góc N = góc A/2
b) đã làm ở bài trên

Chẳng những đối với tam giác mà đối với mọi đa giác lồi,tổng số đo các góc ngoài luôn luôn bằng 360 độ
Ở cuối chương tứ giác (lớp 8),em sẽ học công thức tổng quát tính tổng số đo các góc trong của n-giác lồi (n>=3) là: (n-2).180độ
Góc ngoài tại mỗi đỉnh là góc kề bù với góc trong tại đỉnh đó
Tại n- đỉnh ta có n-góc bẹt là tổng số đo của n-góc TRONG và NGOÀI của n-giác lồi
Vậy tổng số đo n- góc ngoài của n-giác lồi là
n.180độ - (n-2).180độ=2.180độ=360độ
-----------------