
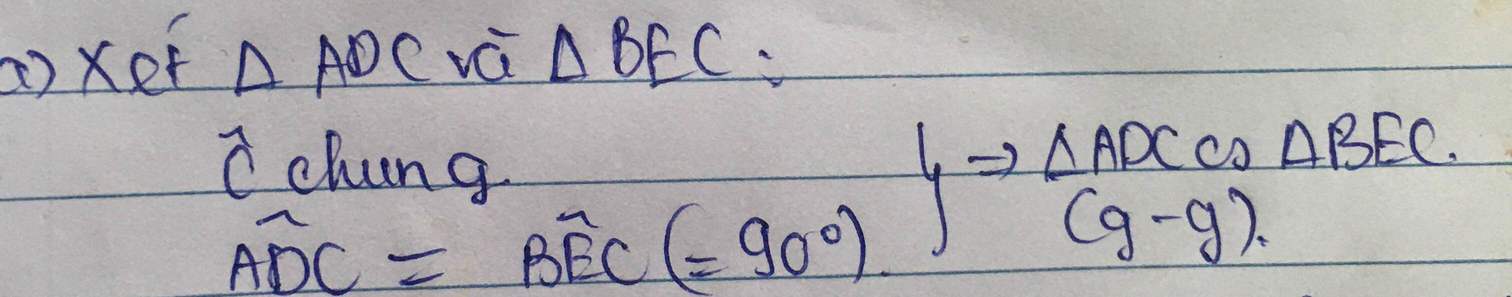
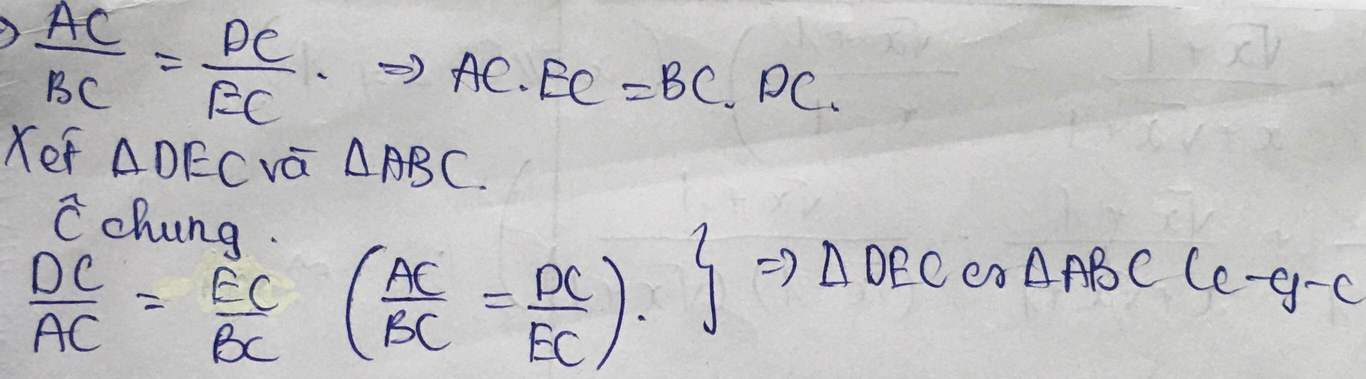
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

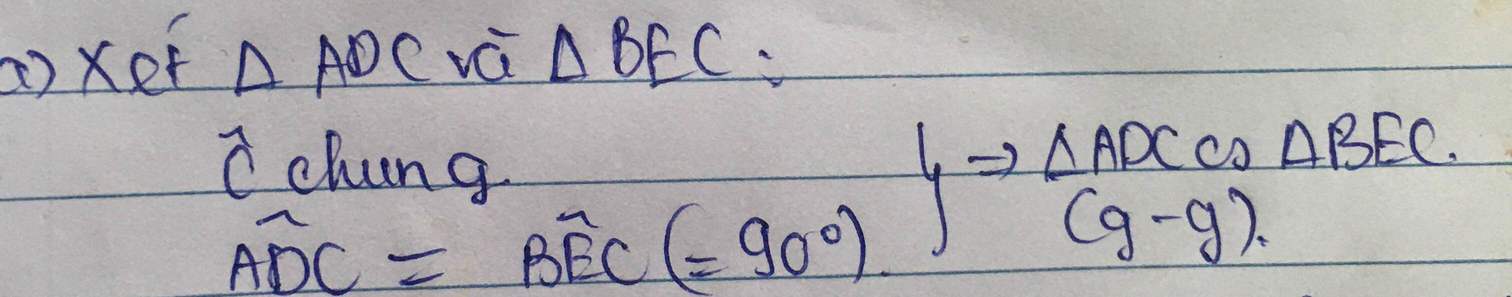
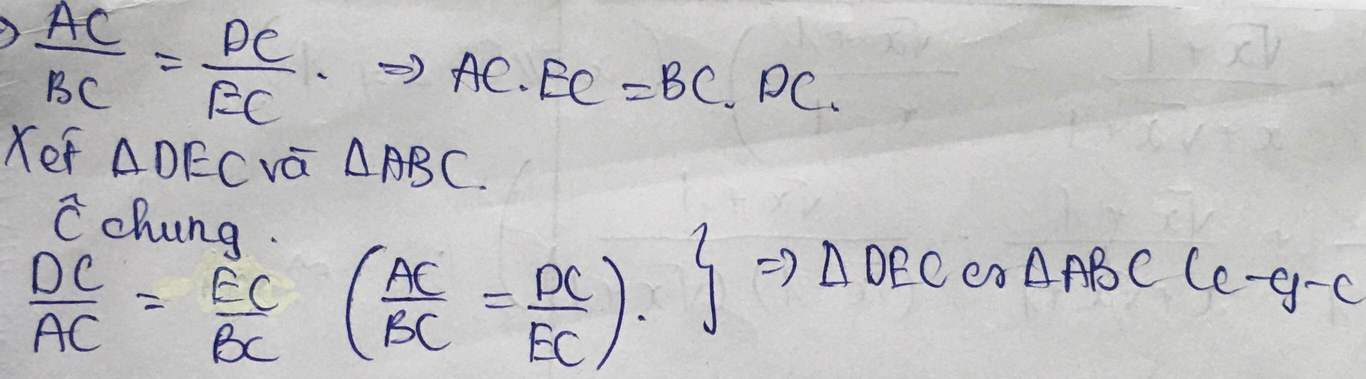

a: Xét ΔCDA vuông tại D và ΔCEB vuông tại E có
góc C chung
Do đó: ΔCDA\(\sim\)ΔCEB
b: Xét ΔHEA vuông tại E và ΔHDB vuông tại D có
\(\widehat{AHE}=\widehat{BHD}\)
Do đó: ΔHEA\(\sim\)ΔHDB
Suy ra: HE/HD=HA/HB
hay \(HE\cdot HB=HD\cdot HA\)


a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100\)
hay BC=10cm
Xét ΔABC có BD là đường phân giác ứng với cạnh AC
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)
mà AD+CD=8
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó: AD=3cm; CD=5cm
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Suy ra: \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
hay \(AB^2=BH\cdot BC\)
c) Ta có: \(\widehat{ABD}=\widehat{DBC}\)( BD là phân giác )\(\Rightarrow90^0-\widehat{ABD}=90^0-\widehat{DBC}\Rightarrow\widehat{BIH}=\widehat{ADI}\Rightarrow\widehat{AID}=\widehat{ADI}\Rightarrow\Delta ADI\) cân tại A\(\Rightarrow AI=AD\Rightarrow\dfrac{AB}{AI}=\dfrac{AB}{AD}\)
Xét Δ ABI và Δ CBD có:
\(\widehat{BAI}=\widehat{BCD}\left(\Delta ABC\sim\Delta HBA\right)\)
\(\dfrac{AB}{AI}=\dfrac{BC}{CD}\left(=\dfrac{AB}{AD}\right)\)
\(\Rightarrow\Delta ABI\sim\Delta CBD\left(c.g.c\right)\)
d) Xét ΔABH có:
BI là tia phân giác của \(\widehat{ABH}\)
\(\Rightarrow\dfrac{IH}{IA}=\dfrac{BH}{AB}\left(1\right)\)( tính chất tia phân giác)
Xét ΔABC có:
BD là tia phân giác của \(\widehat{ABC}\)
\(\Rightarrow\dfrac{AD}{DC}=\dfrac{AB}{BC}\left(2\right)\)( tính chất tia phân giác)
Ta có: \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\left(\Delta ABC\sim\Delta HBA\right)\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\Rightarrow\dfrac{IH}{IA}=\dfrac{AD}{DC}\left(đpcm\right)\)

a: Xét ΔAEH vuông tại E và ΔADC vuông tại D có
góc EAH chung
=>ΔAEH đồng dạng với ΔADC
Xét ΔAFH vuông tại F và ΔADB vuông tại D có
góc FAH chung
=>ΔAFH đồng dạng với ΔADB
b: ΔAEH đồng dạng với ΔADC
=>AE/AD=AH/AC
=>AE*AC=AD*AH
ΔAFH đồng dạng với ΔADB
=>AF/AD=AH/AB
=>AF*AB=AH*AD=AE*AC
c: BH*BE+CH*CF
=BD*BC+CD*BC
=BC^2