Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta thấy \(\widehat{AMN}=\widehat{ABH}+\frac{1}{2}\widehat{BHQ}=\widehat{ACH}+\frac{1}{2}\widehat{CHP}=\widehat{ANM}\). Suy ra \(\Delta AMN\) cân tại A.
b) Dễ thấy tứ giác BEFC và BQPC nội tiếp, suy ra \(\widehat{HEF}=\widehat{HCB}=\widehat{HPQ}\), suy ra EF || PQ
Hiển nhiên \(OA\perp PQ\). Do đó \(OA\perp EF.\)
c) Gọi MK cắt BH tại I, NK cắt CH tại J, HK cắt BC tại S.
Vì A,K là trung điểm hai cung MN của (AMN) nên AK là đường kính của (AMN)
Suy ra \(MK\perp AB,NK\perp AC\)hay MK || CH, NK || BH
Ta có \(\Delta BHQ~\Delta CHP\), theo định lí đường phân giác và Thales thì:
\(\frac{IH}{IB}=\frac{MQ}{MB}=\frac{NP}{NC}=\frac{JH}{JC}\). Suy ra IJ || BC
Cũng từ MK || CH, NK || BH suy ra HIKJ là hình bình hành hay HK chia đôi IJ
Do vậy HK chia đôi BC theo bổ đề hình thang. Vậy HK đi qua S cố định.


a) Giả sử AB < AC. (Các trường hợp khác chứng minh tương tự)
Ta có tam giác CEF cân tại C nên \(\widehat{CEF}=\frac{180^o-\widehat{C}}{2}\)
\(\Rightarrow\widehat{MEB}=\frac{180^o-\widehat{C}}{2}\)
Ta có \(\widehat{MIB}=\widehat{IAB}+\widehat{IBA}=\frac{\widehat{A}+\widehat{B}}{2}=\frac{180^o-\widehat{C}}{2}\)
Hay \(\widehat{MEB}=\widehat{MIB}\). Suy ra tứ giác EMBI là tứ giác nội tiếp.
\(\widehat{IMB}=\widehat{IEB}=90^o\Rightarrow MB\perp AI.\)
b) Chứng minh tương tự \(\widehat{ANI}=90^o\Rightarrow\) tứ giác ANMB nội tiếp đường tròn đường kính AB cố định.
Mà \(\widehat{MBN}=90^o-\widehat{MIB}=\frac{\widehat{ACB}}{2}=\frac{\alpha}{2}=const\)
Do MN là dây cung chắn một góc không đổi trên đường tròn đường kính AB nên độ dài MN không đổi.
c) Gọi O là trung điểm AB thì \(\widehat{MON}=2.\widehat{MBN}=\alpha\)
Do tứ giác IMBD nội tiếp nên \(\widehat{IDM}=\widehat{IBM}=\frac{\alpha}{2}\)
Tương tự : \(\widehat{IDN}=\frac{\alpha}{2}\)
Do đó \(\widehat{MDN}=\alpha=\widehat{NOM}\)
Suy ra tứ giác MNDO nội tiếp hay O thuộc đường tròn ngoại tiếp tam giác DMN.
Do đó đường tròn ngoại tiếp tam giác DMN luôn đi qua điểm O cố định khi C thay đổi.

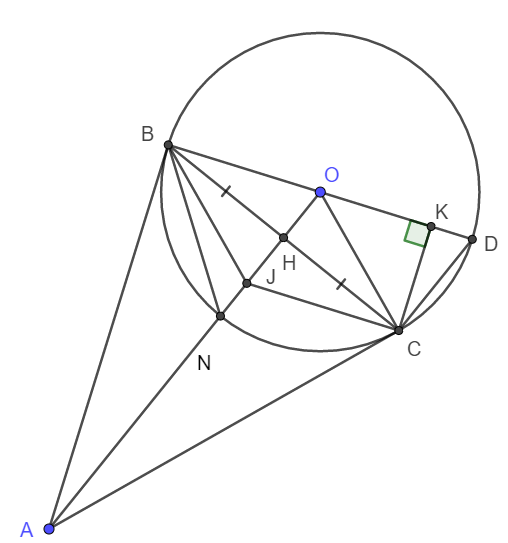
a) Tam giác vuông ABO và ACO có chung cạnh huyền AO nên O, B, A, C cùng thuộc đường tròn đường kính AO.
b) Theo tính chất hai tiếp tuyến cắt nhau, ta có AB = AC nên ABC là tam giác cân tại A.
Lại có AO là phân giác nên đồng thời là đường trung tuyến. Vậy thì AO đi qua H hay A, H, O thảng hàng.
Theo liên hệ giữa góc ở tâm và góc nội tiếp cùng chắn một cung, ta có \(\widehat{KDC}=\frac{\widehat{BOC}}{2}\)
Theo tính chất hai tiếp tuyến cắt nhau ta cũng có: \(\widehat{COA}=\frac{\widehat{BOC}}{2}\)
Suy ra \(\widehat{KDC}=\widehat{COA}\)
Vậy thì \(\Delta KDC\sim\Delta COA\left(g-g\right)\Rightarrow\frac{CK}{AC}=\frac{CD}{AO}\Rightarrow AC.CD=CK.AO\)
c) Ta thấy \(\widehat{ABN}=\widehat{NBC}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung chắn các cung bằng nhau)
Vậy nên BN là phân giác góc ABC.
Lại có AN là phân giác góc BAC nên N là tâm đường tròn nội tiếp tam giác ABC.
d) Gọi J là trực tâm tam giác ABC. Ta có ngay \(JC\perp AB;BJ\perp AC\)
Vậy thì BO // JC ; BJ // OC
Suy ra tứ giác JBOC là hình bình hành.
Lại có OB = OC nên JBOC là hình thoi.
Từ đó ta có JB = JC = OB = OC = R.
Vậy khi A di chuyển trên tia By cố định thì BJ = R hay J thuộc đường tròn tâm B, bán kính R.

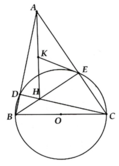
a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm
Gọi P ; M lần lượt là giao điểm của CH và BH với AB và AC
a) Ta có:^CPA = ^BMA = 90o => ^HPA = ^HMA = 90o => ^HPA + ^HMA = 180o
=> Tứ giác HPAM nội tiếp
=> ^PAM + ^PHM = 180o
=> ^BHC = ^PHM = 180o - ^PAM =180o - \(\alpha\)
b) I là tâm đường tròn ngoại tiếp \(\Delta\)HBC
=> IB = IH = IC
=> \(\Delta\)IBH và \(\Delta\)IIHC cân tại I
=> ^IBH = ^IHB và ^ICH = ^IHC
=> ^IBH + ^ICH = ^IHB + ^IHC = ^BHC = \(180^o-\alpha\)
=> ^BIC = 360o - ^IBH - ^ICH - ^BHC = \(2\alpha\)
Ta lại có ^BOC = 2.^BAC = \(2\alpha\) ( góc ở tâm và góc nội tiếp cùng chắn cung BC)
=> ^BIC = ^BOC (1)
Mặt khác: OB = OC; IB = IC
=> OI là đường trung trực của BC (2)
Từ (1) ; (2) => O; I nằm khác phía so với BC
Mà \(\Delta\)BIC cân => IO là đường phân giác ^BIC
=> OIC = \(\frac{1}{2}\).^BIC = \(\alpha\)
c) Từ (b) => ^BIO = ^CIO = ^BOI = ^COI
=> BOCI là hình bình hành có OI vuông BC
=> BOCI là hình thoi
mà B; C; O cố định => I cố định
Tương tự ta cungc chứng minh được: OCJA là hình thoi
=> CJ = CO = R mà C; O cố định
=> J nằm trên đường tròn tâm C bán kính R cố định
d) AJCO là hình thoi => AJ // = OC
OCIB là hình thoi => OC // = BI
=> AJ //=BI
=> AJIB là hình bình hành có hai đường chéo AI; BJ cắt nhau tại N
=> N là trung điểm của AI