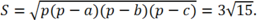Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: Diện tích tam giác là: \(\frac{h_A.a}{2}=\frac{3.6}{2}=9\)(đvdt)
Câu 2: Diện tích tam giác là: \(\frac{1}{2}ab.\sin C=\frac{1}{2}.4.5.\sin60^o=5\sqrt{3}\)(đvdt)
Câu 2: Ta có: \(\hept{\begin{cases}c^2=a^2+b^2-2ab.\cos C\\a^2+b^2>c^2\end{cases}\Rightarrow c^2>c^2-2ab.\cos C\Leftrightarrow2ab.\cos C>0}\)
\(\Rightarrow\cos C>0\Rightarrow C< 90^o\)
Vậy C là góc nhọn

Ta có: \(\widehat A = {15^o},\;\widehat B = {130^o} \Rightarrow \widehat C = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}\)
\( \Rightarrow b = \dfrac{{c.\sin B}}{{\sin C}};\;\;a = \dfrac{{c.\sin A}}{{\sin C}}\)
Mà \(\widehat A = {15^o},\;\widehat B = {130^o},\;\widehat C = {35^o},c = 6\)
\( \Rightarrow b = \dfrac{{6.\sin {{130}^o}}}{{\sin {{35}^o}}} \approx 8;\;\;a = \dfrac{{6.\sin {{15}^o}}}{{\sin {{35}^o}}} \approx 2,7\)
Diện tích tam giác ABC là \(S = \dfrac{1}{2}bc.\sin A = \dfrac{1}{2}.8.6.\sin {15^o} \approx 6,212.\)
Vậy \(a \approx 2,7;\;\,b \approx 8\); \(\widehat C = {35^o}\); \(S \approx 6,212.\)

a) Ta có: \(p = \frac{{a + b + c}}{2} = \frac{{15 + 20 + 25}}{2} = 30\)
Áp dụng công thức heron, ta có: \(S = \sqrt {30.(30 - 15).(30 - 20).(30 - 25)} = 150\)
b) Ta có: \(S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{15.20.25}}{{4.150}} = 12,5.\)

G là trọng tâm tam giác ABC => \(\vec{GA}+\vec{GB}+\vec{GC}=\vec{0}\) => \(\vec{GB}+\vec{GC}=-\vec{GA}\) => \(\left|\vec{GB}+\vec{GC}\right|=\left|-\vec{GA}\right|=GA\)
Tam giác ABC vuông tại nên có trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền BC ; Mà G là trong tâm tam giác nên GA = 2/3 . (1/2. BC) = BC/3 = 5
=> \(\left|\vec{GB}+\vec{GC}\right|=5\)
Đáp án A


Chọn B.
Nửa chu vi của tam giác là p = (4 + 6 + 8) : 2 = 9
Áp dụng công thức Hê-rông
Suy ra: