Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B.
Ta có: A B 2 + A C 2 = B C 2 ( = 100)
Suy ra tam giác ABC vuông tại A.
Do đó, tâm đường tròn ngoại tiếp tam giác ABC là trung điểm cạnh huyền BC.
Đường kính đường tròn là : d = BC = 10cm
Suy ra, bán kính đường tròn ngoại tiếp tam giác ABC là R = d/2 = 5cm

Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
hay BC=13cm
Ta có: ΔABC vuông tại A
nên bán kính đường tròn ngoại tiếp ΔABC là một nửa của cạnh huyền BC
hay \(R=\dfrac{BC}{2}=\dfrac{13}{2}=6.5\left(cm\right)\)
Bài 2:
Ta có: ABCD là hình thang cân
nên A,B,C,D cùng thuộc 1 đường tròn\(\left(đl\right)\)
hay bán kính đường tròn ngoại tiếp ΔABC cũng là bán kính đường tròn ngoại tiếp tứ giác ABCD
Xét ΔABC có
\(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Suy ra: Bán kính của đường tròn ngoại tiếp tứ giác ABCD là \(R=\dfrac{BC}{2}=10\left(cm\right)\)

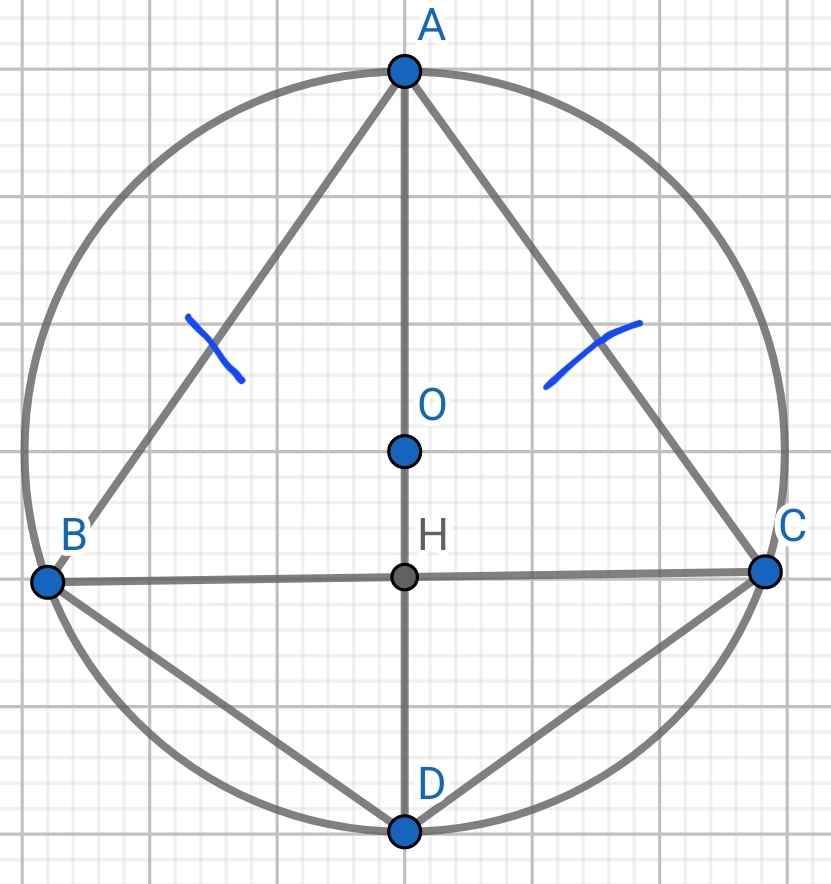
Do (O) là đường tròn ngoại tiếp ∆ABC
⇒ O là giao điểm của ba đường trung trực của ∆ABC
⇒ AO là đường trung trực của ∆ABC
⇒ AO ⊥ BC tại H
⇒ H là trung điểm BC
⇒ BH = BC : 2 = 12 : 2 = 6 (cm)
Do ∠ABD là góc nội tiếp chắn nửa đường tròn
⇒ ∠ABD = 90⁰
∆ABD vuông tại B có BH là đường cao
⇒ 1/BH² = 1/AB² + 1/BD²
⇒ 1/BD² = 1/BH² - 1/AB²
= 1/36 - 1/100
= 4/225
⇒ BD² = 225/4
⇒ BD = 15/2 = 7,5 (cm)
∆ABD vuông tại B
⇒ AD² = AB² + BD² (Pytago)
= 10² + 7,5²
= 156,25
⇒ AD = 12,5 (cm)
Để tính độ dài đoạn thẳng AD, ta cần tìm được tọa độ của điểm D trên đường tròn (O).
Gọi M là trung điểm của đoạn BC. Ta có AM là đường trung trực của BC, do đó OM vuông góc với BC và OM = MC = 6(cm).
Vì tam giác ABC cân tại A nên đường trung trực của BC cũng là đường cao của tam giác. Do đó, ta có AH là đường cao của tam giác ABC và AH = $\sqrt{AB^2 - BM^2}$ = $\sqrt{100 - 36}$ = $\sqrt{64}$ = 8(cm).
Ta có thể tính được AO bằng định lý Pythagoras trong tam giác vuông AOM:
$AO^2 = AM^2 + OM^2 = 10^2 - 6^2 + 6^2 = 100$
Vậy $AO = 10$ (cm).
Do đó, ta có thể tính được bán kính đường tròn (O) là $R = \frac{BC}{2} = 6$ (cm).
Gọi E là điểm đối xứng của A qua đường tròn (O). Ta có AE là đường đối xứng của AH qua đường tròn (O), do đó AE = AH = 8 (cm).
Ta có thể tính được độ dài đoạn thẳng DE bằng định lý Pythagoras trong tam giác vuông AOD:
$DE^2 = DO^2 + OE^2 = R^2 + AE^2 = 6^2 + 8^2 = 100$
Vậy $DE = 10$ (cm).
Ta cần tính độ dài đoạn thẳng AD. Ta có thể tính được độ dài đoạn thẳng HD bằng định lý Euclid:
$\frac{HD}{BD} = \frac{AH}{AB}$
$\Rightarrow HD = \frac{AH \cdot BD}{AB} = \frac{8 \cdot 6}{10} = \frac{24}{5}$ (cm)
Ta có thể tính được độ dài đoạn thẳng AO bằng định lý Pythagoras trong tam giác vuông AHO:
$AD^2 = AO^2 + OD^2 - 2 \cdot AO \cdot OD \cdot \cos{\angle AOD}$
Vì tam giác AOD cân tại O nên $\angle AOD = \frac{1}{2} \cdot \angle AOB$. Ta có thể tính được $\angle AOB$ bằng định lý cosin trong tam giác ABC:
$\cos{\angle AOB} = \frac{AB^2 + AC^2 - BC^2}{2 \cdot AB \cdot AC

a)Ta có: 62+82=102
⇒ AB2+AC2=BC2
⇒ ΔABC vuông tại A (Py-ta-go đảo)
b)Ta có:\(AB^2=BD.BC\Leftrightarrow BD=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6cm\) (hệ thức lượng)
Ta có: \(AC^2=CD.BC\Leftrightarrow CD=\dfrac{AC^2}{BC}=\dfrac{8^2}{10}=6,4cm\) (HTL)
Ta có: \(AD.BC=AB.AC\Leftrightarrow AD=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8cm\) (HTL)
c)Vì P là hình chiếu của D trên AB
⇒DP⊥AB \(\Rightarrow\widehat{APD}=90^o\)
Xét ΔAPD và ΔADB có:
\(\widehat{A}:chung\)
\(\widehat{APD}=\widehat{ADB}=90^o\)
⇒ ΔAPD ∼ ΔADB (g-g)
\(\Rightarrow\dfrac{AP}{AD}=\dfrac{AD}{AB}\Rightarrow AP.AB=AD^2\) (1)
Chứng minh tương tự,ta có: ΔADQ ∼ ΔACD (g-g)
\(\Rightarrow\dfrac{AD}{AC}=\dfrac{AQ}{AD}\Rightarrow AC.AQ=AD^2\) (2)
Ta có: AD2 = BD.CD (HTL) (3)
Từ (1)(2)(3)⇒AP.AB=AC.AQ=BD.CD=AD2
d)Xét tg APDQ có: \(\widehat{DPA}=\widehat{PAQ}=\widehat{AQD}=90^o\)
⇒ APDQ là hình chữ nhật
⇒ AD=PQ và \(\widehat{PDQ}=90^o\)
Ta có: AP.BP=DP2 (HTL trong ΔADB)
AQ.CQ=DQ2 (HTL trong ΔADC)
⇒ AP.BP+AQ.CQ=DP2+DQ2=PQ2 (Py-ta-go trong ΔPDQ vuông tại D)
Mà PQ=AD ⇒ AP.BP+AQ.CQ=AD2
e) Ta có: PQ=AD (cmt)
Mà AD = 4,8 cm
⇒ PQ = 4,8 cm

Áp dụng định lí Pytago cho tam giác vuông ABC, ta có BC=13cm => R=6,5cm

Đáp án là C
Tam giác ABC có:
A B 2 + A C 2 = 12 2 + 16 2 = 400 = B C 2
⇒ ΔABC vuông tại A
⇒ Tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của BC
⇒ Bán kính = 10 cm
Chọn đáp án B.
Ta có: A B 2 + A C 2 = B C 2 ( = 100)
Suy ra, tam giác ABC là tam giác vuông tạiA. Do đó, tâm đường tròn ngoại tiếp tam giác ABC là trung điểm M của BC.
Bán kính đường tròn là: R = BC/2 = 5cm
Chu vi đường tròn ngoại tiếp tam giác ABC là:
C = 2 π . 5 = 10 π (cm)