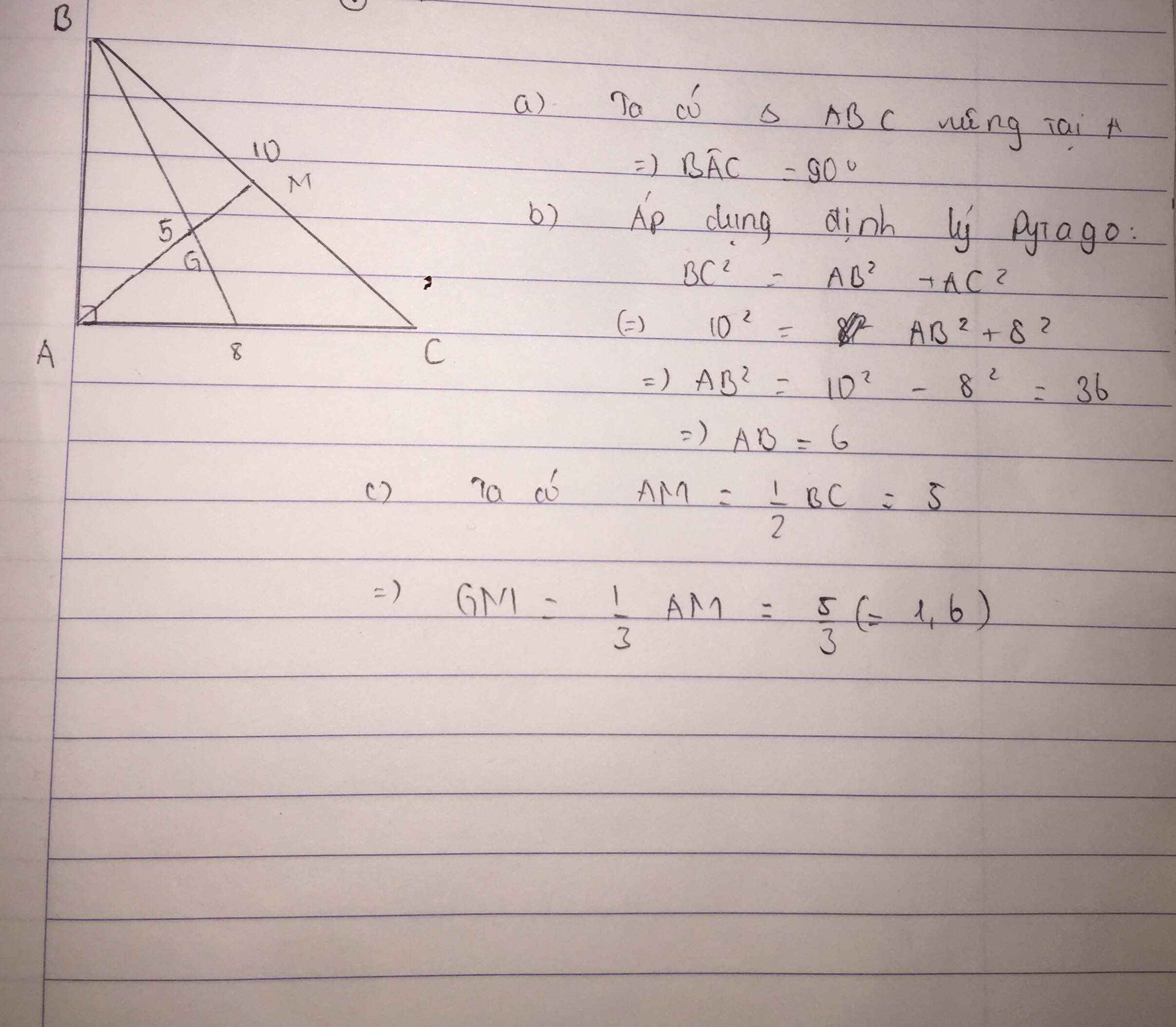Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo tính chất của trọng tâm thì ta có :
\(AG=\frac{2}{3}AM\)
Mà AM = 6cm
\(\Rightarrow AG=\frac{2}{3}.6=4\left(cm\right)\)

a) Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(AM=\dfrac{1}{2}BC\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)

tham khảo
+ Vì MAM là đường trung tuyến của ΔABC(gt)ΔABC(gt)
=> MM là trung điểm của BC.BC.
=> BM=CM=12BCBM=CM=12BC (tính chất trung điểm).
=> BM=CM=12.16=162=8(cm).BM=CM=12.16=162=8(cm).
+ Xét ΔABCΔABC có:
AB=AC=17cm(gt)AB=AC=17cm(gt)
=> ΔABCΔABC cân tại A.A.
Có AMAM là đường trung tuyến (gt).
=> AMAM đồng thời là đường cao của ΔABC.ΔABC.
=> AM⊥BC.AM⊥BC.
+ Xét ΔABMΔABM vuông tại M(cmt)M(cmt) có:
AM2+BM2=AB2AM2+BM2=AB2 (định lí Py - ta - go).
=> AM2+82=172AM2+82=172
=> AM2=172−82AM2=172−82
=> AM2=289−64AM2=289−64
=> AM2=225AM2=225
=> AM=15(cm)AM=15(cm) (vì AM>0AM>0).
+ Vì G là trọng tâm của ΔABC(gt).ΔABC(gt).
=> AG=23AMAG=23AM (tính chất trọng tâm của tam giác).
=> AG=23.15AG=23.15
=> AG=303AG=303
=> AG=10(cm).AG=10(cm).
Vậy AM=15(cm);AG=10(cm).

a: Xét ΔABC có
AM là trung tuyến
AM=BC/2
=>ΔABC vuông tại A
b: AB=căn 10^2-8^2=6cm
c: GM=1/3*AM=5/3(cm)

a: \(BC=\sqrt{18^2+12^2}=3\sqrt{61}\left(cm\right)\)
b: Vì G là trọng tâm
và AM là đường trung tuyến
nên AG=2/3AM=10(cm)