Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\left\{{}\begin{matrix}AB=AC\\BM=MC\\AM\text{ chung}\end{matrix}\right.\Rightarrow\Delta AMB=\Delta AMC\left(c.c.c\right)\\ b,\left\{{}\begin{matrix}BM=MC\\\widehat{AMB}=\widehat{CMD}\left(đđ\right)\\AM=MD\end{matrix}\right.\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\\ \Rightarrow\widehat{ABC}=\widehat{BCD}\\ \text{Mà 2 góc này ở vị trí slt nên }AB\text{//}CD\\ c,\left\{{}\begin{matrix}BM=MC\\\widehat{AMC}=\widehat{BMD}\\AM=MD\end{matrix}\right.\Rightarrow\Delta AMC=\Delta DMB\left(c.g.c\right)\\ \Rightarrow\widehat{ACB}=\widehat{CBD}\\ \text{Mà 2 góc này ở vị trí slt nên }AC\text{//}BD\)

a) Sửa đề: ΔAMB=ΔDMC
Xét ΔAMB và ΔDMC có
MA=MD(gt)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔDMC(c-g-c)

Xét \(\Delta AMB\)VÀ \(\Delta AMC\)
AB=AC(gt)
<B=<C(tam giác ABC cân)
BM=MC(gt)
\(\Rightarrow\Delta AMB=\Delta AMC\left(c-g-c\right)\)
Xét \(\Delta AMB\)và\(\Delta CMD\)có:
<AMB=<CMD(đối đỉnh)
AM=MD(gt)
MB=MC(gt)
\(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)
=>góc BAM=<CDM(2 góc tương ướng)
mà hai góc này ở vị trí so le trong
=> AB//CD

a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: ta có: ΔAMB=ΔDMC
nên AB=DC

a,
Xét △ABC có:
BC2 = 172 = 289
AB2 + AC2 = 152 + 82 = 225 + 64 = 289
=> BC2 = AB2 + AC2
=> △ABC vuông
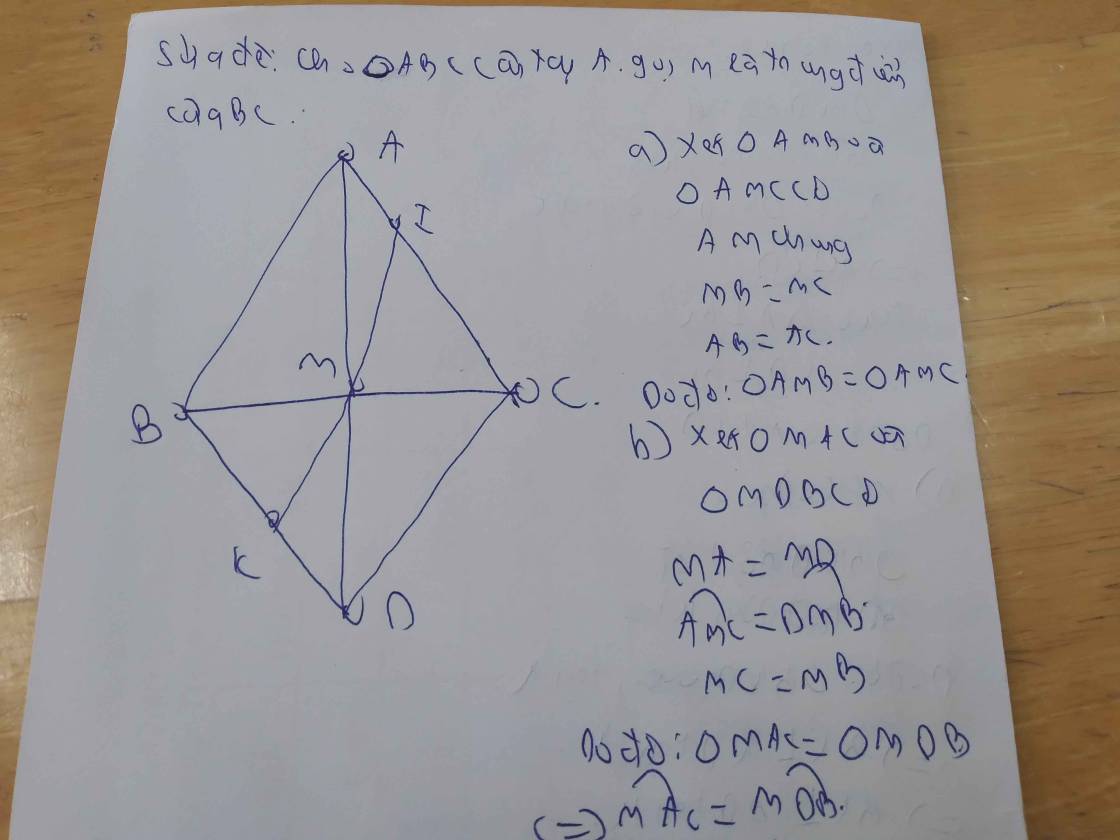

Bn tự vẽ hình
a) Xét Δ AMB và Δ AMC
AB=AC
BM=MC
AM chung
⇒ Δ AMB = Δ AMC
b) Xét Δ AMB và Δ DMC
DM=AM
BM=CM
AMB=CMD (đối đỉnh)
⇒ Δ AMB = Δ DMC
⇒ ABM=DCM (2 góc t.ứng)
Mà 2 góc này ở vị trí SLT
⇒ AB//CD
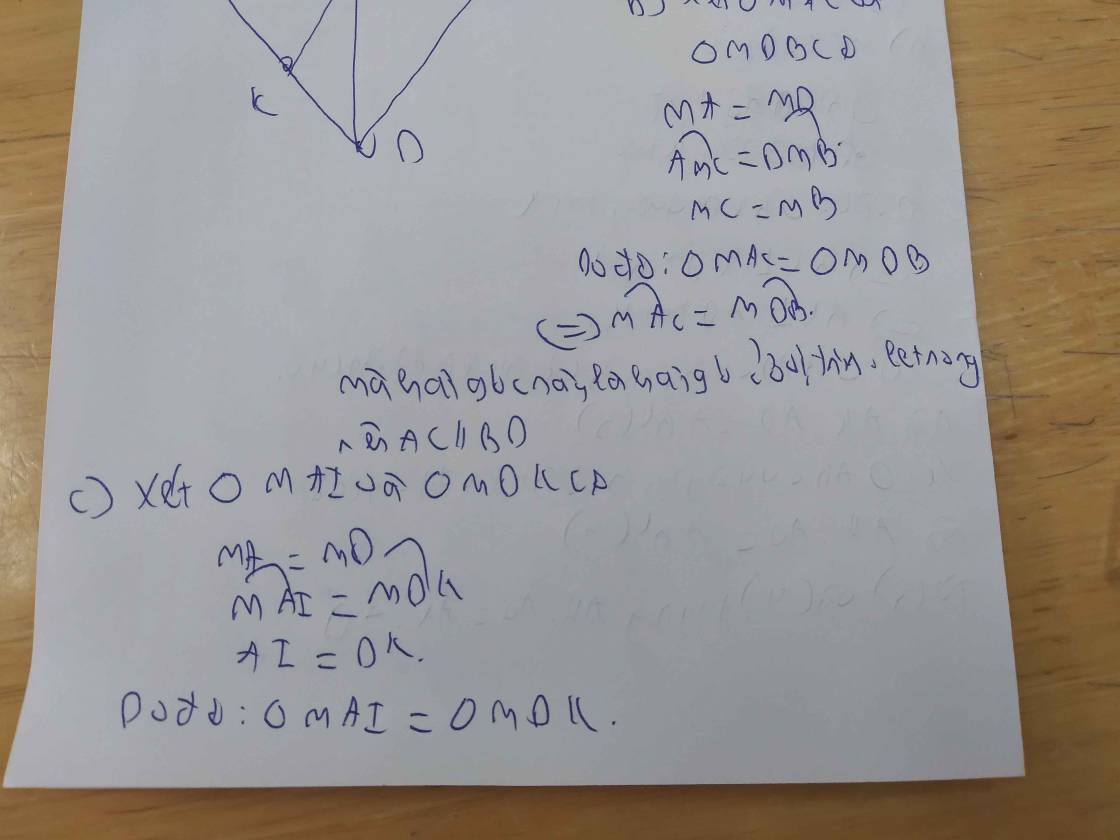
c) Bn tự lm, tương tự phần b)
a) Xét tam giác AMB và tam giác AMC có:
+ AB = AC (gt).
+ MB = MC (M là trung điểm của BC).
+ AM chung.
=> Tam giác AMB = Tam giác AMC (c - c - c).
b) Xét tứ giác ABCD có:
+ M là trung điểm của BC (gt).
+ M là trung điểm của AD (MD = MA).
=> Tứ giác ABCD là hình bình hành (dhnb).
=> AB // CD (Tính chất hình bình hành).
c) Tứ giác ABCD là hình bình hành (cmt).
=> AC // BD (Tính chất hình bình hành).