a: Xét ΔABC có 

E là trung điểm của AB

K là trung điểm của AC

Do đó: KE là đường trung bình của ΔABC

c: Ta có: KE là đường trung bình của ΔBAC

nên \(KE=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)

a: Xét ΔABC có

E là trung điểm của AB

K là trung điểm của AC

Do đó: EK là đường trung bình của ΔBAC

a: Xét ΔABC có

E là trung điểm của AB

K là trung điểm của AC

Do đó: EK là đường trung bình của ΔBAC

Suy ra: \(EK=\dfrac{BC}{2}\)

c: \(EK=\dfrac{10}{2}=5\left(cm\right)\)

a: Xét ΔABC có

E là trung điểm của AB

K là trung điểm của AC

=>: EK là đường trung bình của ΔABC (Đ.N)

b: Xét  ΔABC , ta có :

 EK là đường trung bình của ΔABC 

=> EK // BC (ĐL.2)

Xét  ΔAHC , ta có 

AK = KC (gt)

IK // HC ( vì EK // BC mà I thuộc EK , H thuộc BC , gt)

=> AI = IH , (ĐL,1)

=> I là trung điểm của AH 

c : Ta có , BC = 10 cm (gt)

Mà EK là đường trung bình của tam giác ABC (theo a)

=> EK = 1/2 BC (ĐL.2)

Vậy EK = 1/2.10 = 5 (cm)

=> EK = 5 (cm)

Hình bạn tự vẽ nhé ;)))

a: Xét ΔABC có

E là trung điểm của AB

K là trung điểm của AC

Do đó: EK là đường trung bình của ΔABC

b: Xét tứ giác BEKC có KE//BC

nên BEKC là hình thang

mà \(\widehat{EBC}=\widehat{KCB}\)

nên BEKC là hình thang cân

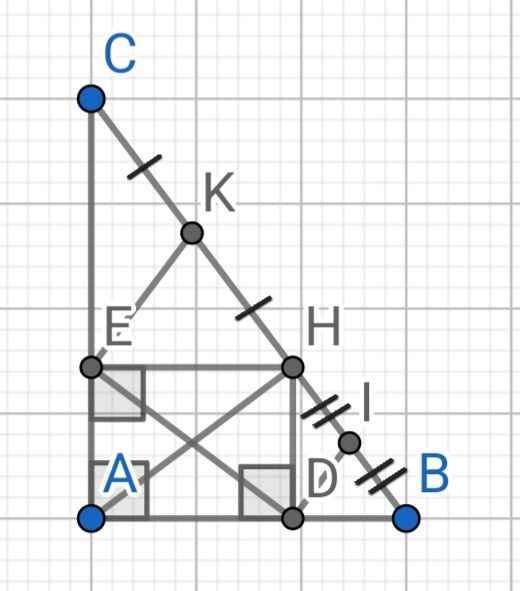   a) Tứ giác ADHE có:

∠AEH = ∠ADH = ∠HAE = 90⁰ (gt)

⇒ ADHE là hình chữ nhật

⇒ AH = DE

b) BHD vuông tại D

I là trung điểm của HB (gt)

⇒ ID = IH = BH : 2

⇒ ∆IDH cân tại I

⇒ ∠IDH = ∠IHD

⇒ ∠HID = 180⁰ - (∠IDH + ∠IHD)

= 180⁰ - 2∠IHD (1)

∆CEH vuông tại E

K là trung điểm HC (gt)

⇒ KE = KC = HC : 2

⇒ ∆KEC cân tại K

⇒ ∠KEC = ∠KCE

⇒ ∠CKE = 180⁰ - (∠KEC + ∠KCE)

= 180⁰ - 2∠KEC (2)

Do HD ⊥ AB (gt)

AC ⊥ AB (gt)

⇒ HD // AC

⇒ ∠IHD = ∠KCE (đồng vị)

⇒ 2∠IHD = 2∠KCE (3)

Từ (1), (2) và (3) ⇒ ∠CKE = ∠HID

Mà ∠CKE và ∠HID là hai góc đồng vị

⇒ DI // KE

a: Xét ΔAHB có 

E là trung điểm của AB

EK//AH

Do đó: K là trung điểm của BH

hay BK=HK

b: Xét ΔABC có 

E là trung điểm của AB

F là trung điểm của AC

Do đó: FE là đường trung bình của ΔABC

Suy ra: FE//BC và \(EF=\dfrac{BC}{2}\)

hay BC=2EF và EFCB là hình thang