Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

áp dụng t/c đường phân giác vào tam giác AMB có :
\(\dfrac{ME}{AB}=\dfrac{AM}{MB}\left(1\right)\)
áp dụng t/c đường phân giác vào tam giác AMC có :
\(\dfrac{MF}{AC}=\dfrac{AM}{MC}\left(2\right)\)
mà AB = AC ; MB=MC
từ (1) và (2) suy ra : ME= MF (đpcm)

Vì ME là phân giác của \(\widehat{AMB}\) nên \(\frac{EA}{EB}=\frac{MA}{MB}\)
MF là phân giác của \(\widehat{AMC}\) nên \(\frac{FA}{FB}=\frac{MA}{MC}\)
Mà \(MB=MC\) nên \(\frac{EA}{EB}=\frac{FA}{FC}\). Theo định lí Ta - lét đảo \(\Rightarrow EF\)// \(BC\)
\(\Rightarrow\widehat{FEM}=\widehat{EMB}\)
\(\widehat{EFM}=\widehat{FMC}\)
Mà \(\widehat{FEM}=\widehat{EFM}\) ( Do \(\Delta MEF\) cân tại M )
\(\Rightarrow\widehat{EMB}=\widehat{FMC}\Rightarrow\frac{\widehat{AMB}}{2}=\frac{\widehat{AMC}}{2}\Rightarrow\widehat{AMB}=\widehat{AMC}=90\)
=> AM vuông góc với BC hay AM là đường cao .lại có AM là trung tuyến nên tam giác ABC cân tại A

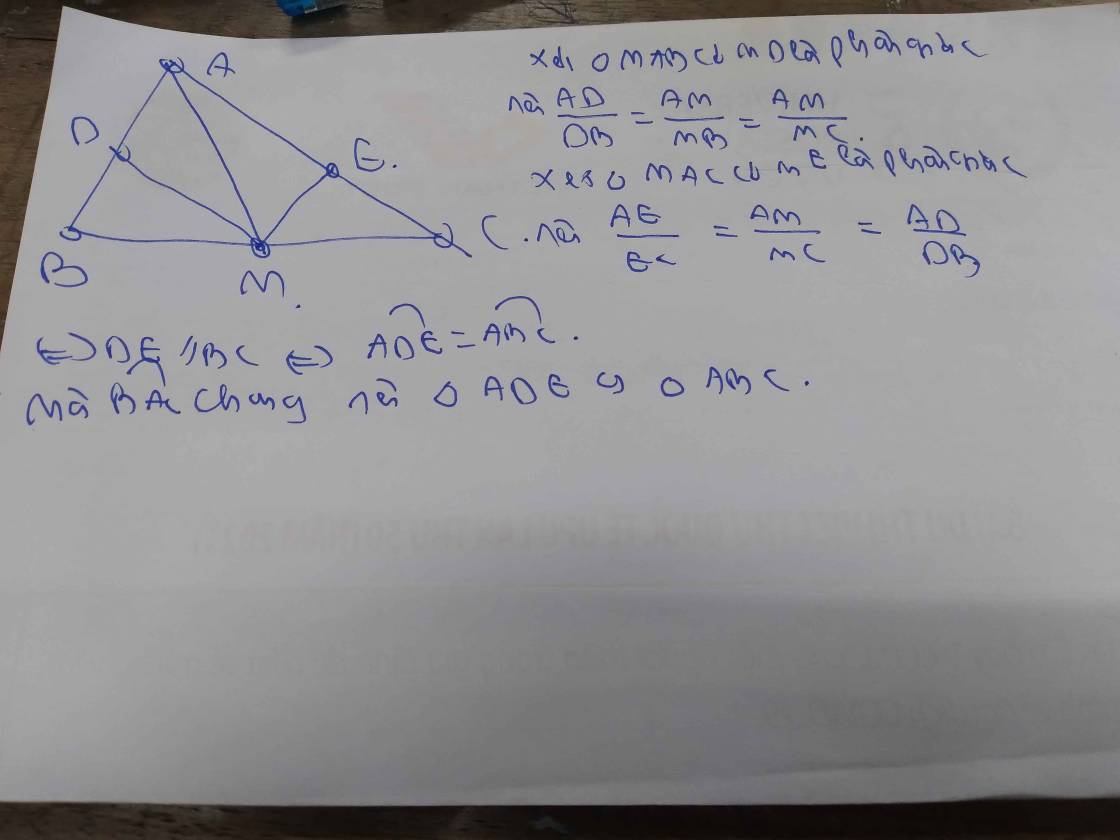
Xet ΔMAB có MD là phân giác
nên AD/DB=AM/MB=AM/MC
Xét ΔMAC có ME là phân giác
nên AE/EC=AM/MC
=>AD/DB=AE/EC
=>DE//BC
=>ΔADE đồng dạng với ΔABC

Áp dụng định lý phân giác cho tam giác ABM:
\(\dfrac{AM}{BM}=\dfrac{AD}{BD}\) (1)
Áp dụng định lý phân giác cho tam giác ACM:
\(\dfrac{AM}{CM}=\dfrac{AE}{CE}\) (2)
Mà AM là trung tuyến \(\Rightarrow BM=CM\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{AD}{BD}=\dfrac{AE}{CE}\Rightarrow\dfrac{AD}{AD+BD}=\dfrac{AE}{AE+CE}\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
\(\Rightarrow DE||BC\) (định lý talet đảo)
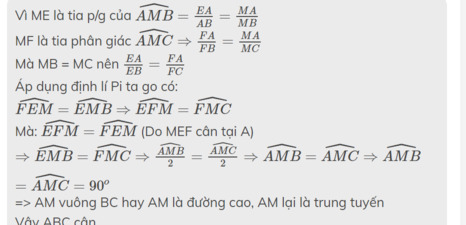
Ghi rõ ra bạn ơi ko Hải nó đập :v