Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: góc BFC=góc BEC=90 độ
=>BFEC nộitiếp
Tâm là trung điểm của BC
2: góc EFC=góc DAC
góc DFC=góc EBC
góc DAC=góc EBC
=>góc EFC=góc DFC
=>FC là phân giác của góc EFD
BFEC nội tiếp
=>góc AFE=góc ACB
mà góc A chung
nên ΔAFE đồng dạng với ΔACB
=>AF/AC=AE/AB
=>AF*AB=AC*AE

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: góc DFC=góc EBC
góc EFC=góc DAC
góc EBC=góc DAC
=>góc DFC=góc EFC

a: Xét (O) có
ΔAHF nội tiếp
AH là đường kính
Do đó; ΔAHF vuông tại F
Suy ra: HF\(\perp\)AB
mà CH\(\perp\)AB
nên C,H,F thẳng hàng
b: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BEFC là tứ giác nội tiếp

a) Xét tứ giác KEDC có
\(\widehat{KEC}=\widehat{KDC}\left(=90^0\right)\)
\(\widehat{KEC}\) và \(\widehat{KDC}\) là hai góc cùng nhìn cạnh KC
Do đó: KEDC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
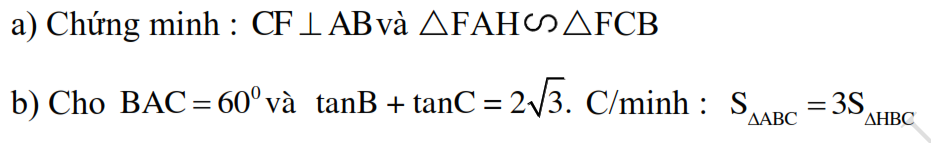

a: Xét ΔBAC có
AD là đường cao ứng với cạnh BC
BE là đường cao ứng với cạnh AC
AD cắt BE tại H
Do đó: H là trực tâm của ΔBAC
Suy ra: CH\(\perp\)AB tại F
Xét ΔFAH vuông tại F và ΔFCB vuông tại F có
\(\widehat{FAH}=\widehat{FCB}\left(=90^0-\widehat{FBC}\right)\)
Do đó: ΔFAH\(\sim\)ΔFCB