Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 : Bài giải
Hình tự vẽ //
a) Ta có DOC = cung DC
Vì DOC là góc ở tâm và DAC là góc chắn cung DC
=>DOC = 2 . AOC (1)
mà tam giác AOC cân =>AOC=180-2/AOC (2)
Từ (1) ; (2) ta được DOC + AOC = 180
b) Góc ACD là góc nội tiếp chắn nữa đường tròn
=>ACD=90 độ
c) c) HC=1/2*BC=12
=>AH=căn(20^2-12^2)=16
Ta có Sin(BAO)=12/20=>BAO=36.86989765
=>AOB=180-36.86989765*2=106.2602047
Ta có AB^2=AO^2+OB^2-2*OB*OA*cos(106.2602047)
<=>AO^2+OA^2-2OA^2*cos(106.2602047)=20^2
=>OA=12.5

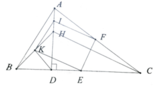
a, Chứng minh IFEK là hình bình hành có tâm O. Chứng minh IK ⊥ KE => IFEKlà hình chữ nhật => I,F,E,K cùng thuộc (O;OI)
b, Ta có: I D E ^ = 90 0 => Tam giác IDE vuông tại D
Chứng minh rằng KD ⊥ DF => ∆ KDF vuông

a/
+ Xét tg AHB có
IA=IH (đề bài)
KB=KH (đề bài)
=> IK là đường trung bình của tg ABH => IK//=AB/2 (1)
+ Xét tam giác ABC có
FA=FC (đề bài)
EB=EC (đề bài)
=> EF là đường trung bình của tg ABC => EF//=AB/2 (2)
Từ (1) và (2) => Tứ giác KIFE là hình bình hành) (3)
+ Xét tam giác BHC có
KB=KH
EB=EC
=> KE là đường trung bình của tg BHC => KE//HC
mà HC vuông góc với AB (H là trực tâm)
=> KE vuông góc với AB
Ta đã c/m ở trên là IK//AB
=> IK vuông góc với KE (4)
Từ (3) và (4) => KIFE là hình chữ nhật (hình bình hành có 1 góc vuông là HCN)
+ Ta có K và F cùng nhìn IE dưới 1 góc vuông => K; F nằm trên đường tròn đường kings IE => E; F; I; K cùng nằm trên 1 đường tròn đường kính IE
b/ Ta có AD vuông góc BC => D cũng nhìn IE dưới 1 góc vuông => D thuộc đường tròn đường kính IE

AK giao BC tại F'
->ABF' = ABH + HAF' = ACB + CAF' = 180 - AF'C = AF'B nên AB = BF'. Mà AB = BF =>F trùng F'
Vậy A, K, F thẳng hàng