Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi AH là đường cao của tam giác ABC
Diện tích ABC lúc đầu là:
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=180\)
Theo đề, ta có: \(\dfrac{1}{2}\cdot AH\cdot\left(BC+4\right)=180+24\)
=>\(\dfrac{1}{2}\cdot AH\cdot BC+2\cdot AH=204\)
=>\(2\cdot AH=204-180=24\)
=>AH=12(cm)
=>BC=2*180/12=360/12=30(cm)

Chiều cao là
35x2:5=14 (m)
Đáy BC của tam giác là
150x2:14=150/7 (m)
Đ/S:150/7 m
Chiều cao là
35 x 2 : 5 = 14 (m)
Đáy BC hình tam giác là :
150 x 2 : 14 = \(\frac{150}{7}\)
Đ/S :\(\frac{150}{7}\)

Cách 1 : Từ A kẻ đường cao AH của ∆ ABC thì AH cũng là đường cao của
∆ ABD
Đường cao AH là :
37,5 x 2 : 5 = 15 (cm)
Đáy BC là :
150 x 2 : 15 = 20 (cm)
Đáp số 20 cm.
Cách 2 :
Từ A hạ đường cao AH vuông góc với BC . Đường cao AH là đường cao chung của hai tam giác ABC và ABD . Mà : Tỉ số 2 diện tích tam giác là :
S Δ ABCS Δ ABD=15037,5=4 S ∆ ABCS ∆ ABD=15037,5=4
Hai tam giác có tỉ số diện tích là 4 mà chúng có chung đường cao,nên tỉ số 2 đáy cũng là 4. Vởy đáy BC là :
5 x 4 = 20 (cm)
Đáp số 20 cm.

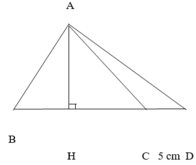
Cách 1 : Từ A kẻ đường cao AH của ∆ ABC thì AH cũng là đường cao của
∆ ABD
Đường cao AH là :
37,5 x 2 : 5 = 15 (cm)
Đáy BC là :
150 x 2 : 15 = 20 (cm)
Đáp số 20 cm.
Cách 2 :
Từ A hạ đường cao AH vuông góc với BC . Đường cao AH là đường cao chung của hai tam giác ABC và ABD . Mà : Tỉ số 2 diện tích tam giác là :
S ∆ A B C S ∆ A B D = 150 37 , 5 = 4
Hai tam giác có tỉ số diện tích là 4 mà chúng có chung đường cao,nên tỉ số 2 đáy cũng là 4. Vởy đáy BC là :
5 x 4 = 20 (cm)
Đáp số 20 cm.
Đáp án: 20 cm
Giải thích các bước giải:
Chiều cao tam giác ABC là
37,5 x 2 : 5 = 15 (cm)
Đáy BC dài số cm là
150 x 2 : 15 = 20 (cm)
Đáp số 20 cm