Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC có:
M là trung điểm của AB (GT)
P là trung điểm của BC (GT)
=> MP là đường trung bình tam giác ABC
=> MP = \(\frac{1}{2}\)AC
=> Diện tích MNP = \(\frac{1}{2}\)diện tích ABC
= \(\frac{1}{2}.24\)= 12 (cm2)

Vẽ hình vào nha
a) SAMC=1/2SABC( Vì có đáy MC=1/2 BC và có chung chiều cao hạ từ đỉnh A xuống BC)
=> SAMC=36:2=18(cm2)
b)* SABE=1/2SABC( Vì có đáy AE=1/2 AC và có chung chiều cao hạ từ đỉnh B xuống AC)
=> SABE=36:2=18(cm2)
*SAOE=1/2SABE( Vì có đáy OE=1/2 BE và có chung chiều cao hạ từ đỉnh A xuống BE)
=> SAOE=18:2=9(cm2)
Đáp số: a)18cm2
b)9cm2
@Teoyewmay

Vì M là trung điểm của AB nên:
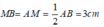
Áp dụng định lí py tago vào tam giác ABC có:
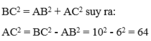
Suy ra: AC = 8cm
Xét tam giác ABC có M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC nên: MN// AC và
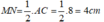
Suy ra: tứ giác MNCA là hình thang vuông.
Diện tích hình thang MNCA là:
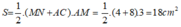
Chọn đáp án D

Câu hỏi của Hoa Thân - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài tương tự tại đây nhé.

\(S_{ABM}=S_{ACM}=12\left(cm^2\right)\)
=>\(S_{BNM}=\dfrac{2}{3}\cdot12=8cm^2;S_{NMC}=8cm^2\)
=>\(S_{BNC}=16\left(cm^2\right)\)
Answer:
Bạn tự vẽ hình.
Ta xét tam giác ABC
\(IB=AI=\frac{1}{2}AB\)
\(NC=AN=\frac{1}{2}AC\)
=> IN là đường trung bình
\(\Rightarrow IN=\frac{1}{2}BC\)
Tương tự ta chứng minh được
MN và MI là đường trung bình của tam giác ABC
\(\Rightarrow MI=\frac{1}{2}AC\) và \(MN=\frac{1}{2}AB\)
Ta xét tam giác MNI và tam giác ABC
\(\frac{MN}{AB}=\frac{NI}{BC}=\frac{MI}{AC}=\frac{1}{2}\)
Do vậy tam giác MNI ~ tam giác ABC (c.c.c)
\(\Rightarrow\frac{S_{\Delta MNI}}{S_{\Delta ABC}}=\left(\frac{MN}{AB}\right)^2=\frac{1}{4}\)
\(\Rightarrow S_{\Delta MNI}=\frac{1}{4}S_{\Delta ABC}=\frac{1}{4}.24=6cm^2\)
Xét tam giác ABC có:
M là trung điểm của AB (GT)
P là trung điểm của BC (GT)
=> MP là đường trung bình tam giác ABC
=> MP = 1212AC
=> Diện tích MNP = 1212diện tích ABC
= 12.2412.24= 12 (cm2)