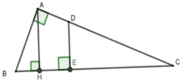
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.

Xét ΔAHC và ΔABC có C chung và A H C ^ = B A C ^ = 90 ∘ nên ΔAHC ~ ΔBAC (g-g)

Ta có S D E C = 1 2 S A B C (1), S A H C : S A B C = 18 25 (2).

Từ (1) và (2) suy ra

S D E C : S A H C = 1 2 : 18 25 = 25 36 = ( 5 6 ) 2   3

Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên

S D E C : S A H C = ( E C H C ) 2 (4)

Từ (3) và (4) suy ra E C H C = 5 6  tức là E C 18 = 5 6 => EC = 15cm.

Đáp án: A

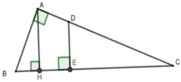
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.

Xét ΔAHC và ΔABC có C chung và A H C ^ = B A C ^ = 90 ∘ nên ΔAHC ~ ΔBAC (g-g)

Ta có S D E C = 1 2 S A B C (1), S A H C : S A B C = H C B C = 9 9 + 3 , 5 = 18 25 2

Từ (1) và (2) suy ra S D E C : S A H C = 1 2 : 18 25 = 25 36 = ( 5 6 ) 2 ( 3 )

Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên

S D E C : S A H C = ( E C H C ) 2 ( 4 )

Từ (3) và (4) suy ra E C H C = 5 6  tức là E C 9 = 5 6  => EC = 7,5cm.

Đáp án: D

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A

Ta có: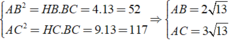

Vậy S A B C   =   1 2 A B . A C   =   1 2 . 2 13   . 3 13 =   39 c m 2

Chọn đáp án A.

3: 

\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)

HB=12^2/20=7,2cm

=>HC=20-7,2=12,8cm

\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)

\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có

góc B chung

=>ΔHBA đồng dạng với ΔABC

b: BC=căn 15^2+20^2=25cm

AH=15*20/25=12cm