Tương tự, HS tự làm

a)Áp dụng HTL2 vào tam giác ABC cuông tại A, đường cao AH ta có:

AH²=BH.HC=9.16=144

<=>AH=√144=12((cm)

Áp dụng định lý Pytago vào tam giác vuông BHA ta có:

BA²=AH²+BH²=12²+9²=225

<=>BA=√225=15(cm)

Áp dụng định lý Pytago vào tam giác vuông CHA ta có:

CA²=AH²+CH²=12²+16²=20(cm)

Vậy AB=15cm,AC=20cm,AH=12cm

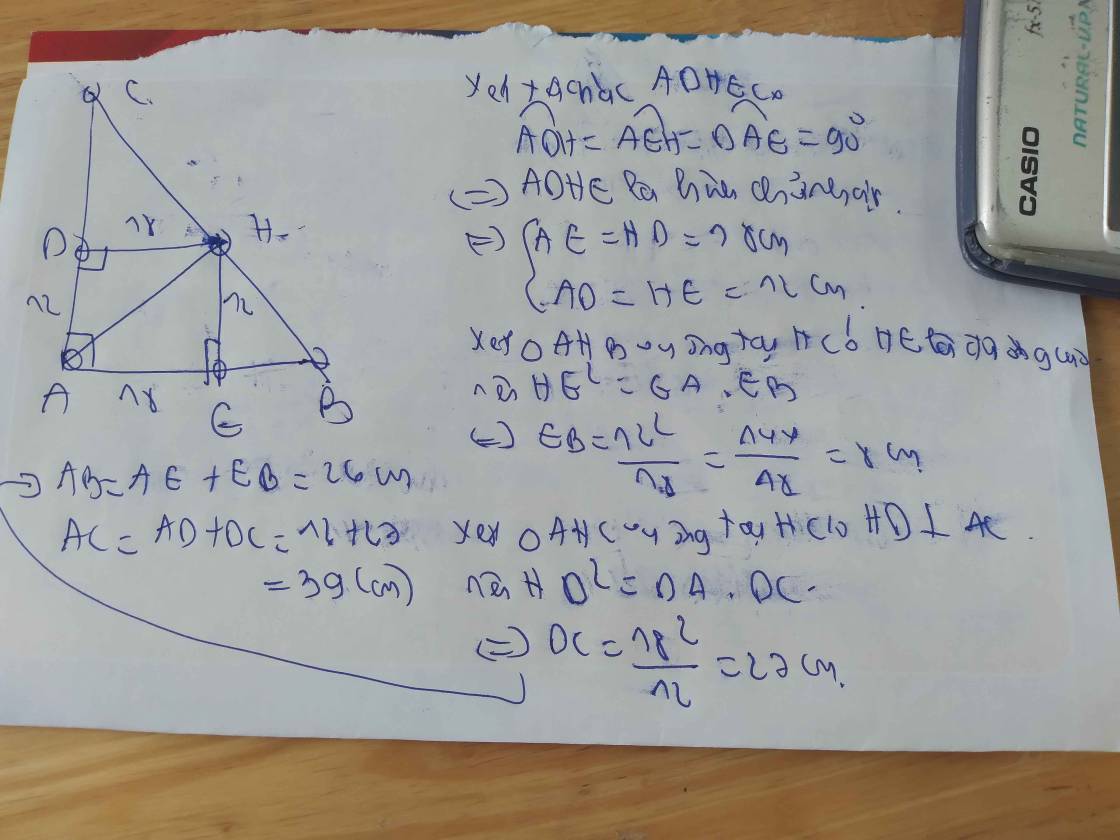
Dễ dàng chứng minh được:  \(HEAD\)là hình chữ nhật

\(\Rightarrow\)\(HE=AD=12\)

          \(HD=EA=18\)

Áp dụng hệ thức lượng ta có:

       \(HD^2=AD.DC\)

\(\Rightarrow\)\(DC=\frac{HD^2}{AD}\)

\(\Rightarrow\)\(DC=\frac{18^2}{12}=27\)

\(\Rightarrow\)\(AC=AD+DC=12+27=39\)

            \(HE^2=BE.AE\)

\(\Rightarrow\)\(BE=\frac{HE^2}{AE}\)

\(\Rightarrow\)\(BE=\frac{12^2}{18}=8\)

\(\Rightarrow\)\(AB=BE+EA=8+18=26\)

Xét ΔHAB vuông tại H có HE là đường cao

nên \(AE\cdot AB=AH^2\)

Xét ΔHAC vuông tại H có HF là đường cao

nên \(AF\cdot AC=AH^2\)

\(S_{AEF}=\dfrac{1}{16}\cdot S_{ABC}\)

=>\(\dfrac{1}{2}\cdot AE\cdot AF=\dfrac{1}{16}\cdot\dfrac{1}{2}\cdot AB\cdot AC\)

=>\(AE\cdot AF=\dfrac{1}{16}\cdot AB\cdot AC\)

=>\(\dfrac{AH^2}{AB}\cdot\dfrac{AH^2}{AC}=\dfrac{1}{16}\cdot AB\cdot AC\)

=>\(AH^4=\dfrac{1}{16}\cdot AB^2\cdot AC^2\)

=>\(AH^2=\dfrac{1}{4}\cdot AB\cdot AC=\dfrac{1}{4}\cdot AH\cdot BC\)

=>\(AH=\dfrac{1}{4}\cdot BC\)

Gọi M là trung điểm của BC

=>AH vuông góc HM tại H

ΔABC vuông tại A

mà AM là đường trung tuyến

nên \(AM=\dfrac{1}{2}BC\)=MB=MC

=>\(\dfrac{AH}{AM}=\dfrac{1}{2}\) và ΔMAC cân tại M

Xét ΔAHM vuông tại H có

\(sinAMH=\dfrac{AH}{AM}=\dfrac{1}{2}\)

=>\(\widehat{AMB}=30^0\)

=>\(\widehat{AMC}=150^0\)

ΔMAC cân tại M

=>\(\widehat{MCA}=\dfrac{180^0-\widehat{AMC}}{2}=15^0\)

=>\(\widehat{ACB}=15^0\)

AC=căn 10^2-8^2=6cm

AH=6*8/10=4,8cm

AE=AH^2/AB=4,8^2/8=2,88cm

AF=AH^2/AC=4,8^2/6=3,84cm

S AEF=1/2*2,88*3,84=5,5296cm2

S ABC=1/2*6*8=24cm²

=>S BEFC=24-5,5296=18,4704cm²

Đề sai rồi bạn

Cho tam giác ABC vuông tại A , đường cao AH (H thuộc BC)

a) Tính BH , AH biết AB =20cm , BC= 25cm

b) Từ B kẻ đường thẳng vuông góc với đường trung tuyến AD của tam giác AD của tam giác ABC tại E cắt Ac tại F . Chứng minh : tam giác BHF đồng dạng với tam giác BEC 

giải giúp em với ạ

a: BC=BH+CH=25cm

Xét ΔABC vuông tại A có AH là đường cao

nên AB^2=BH*BC; AC^2=CH*BC; AH^2=HB*HC

\(AB=\sqrt{BH\cdot BC}=\sqrt{9\cdot25}=15\left(cm\right)\)

\(AC=\sqrt{16\cdot25}=20\left(cm\right)\)

\(AH=\sqrt{HB\cdot HC}=12\left(cm\right)\)

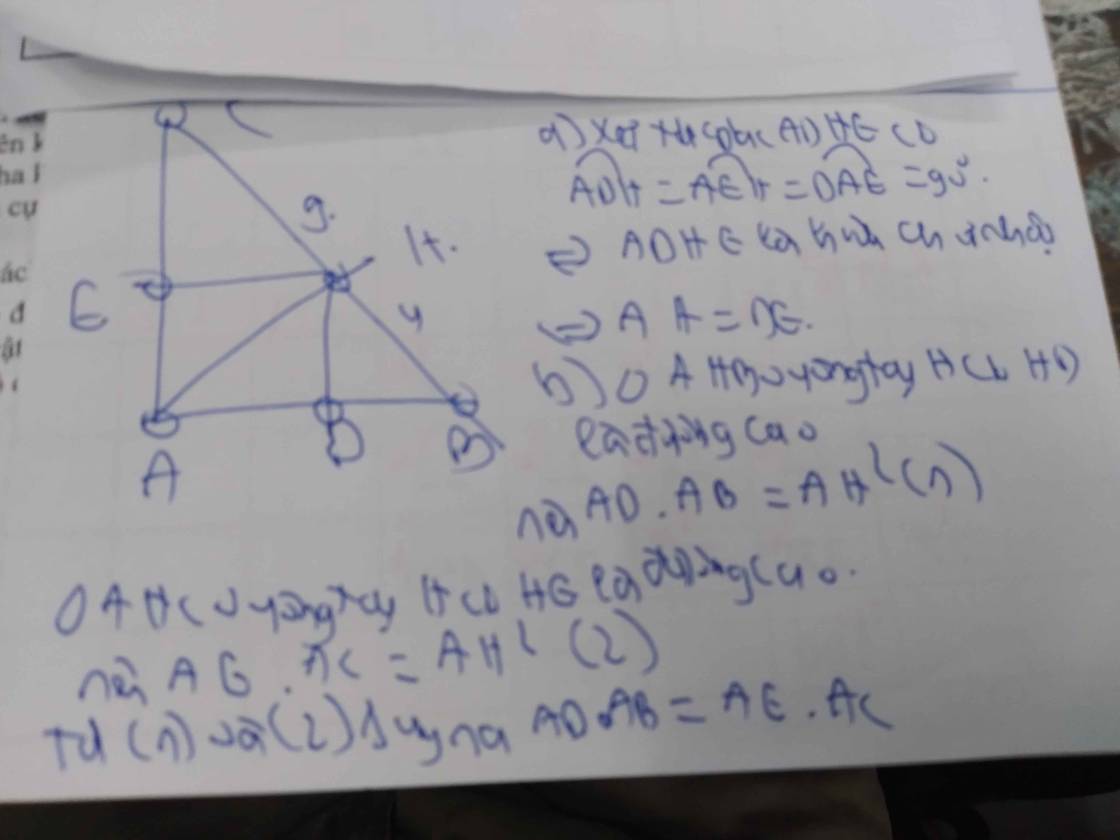
b: Xét tứ giác ADHE có

góc ADH=góc AEH=góc DAE=90 độ

=>ADHE là hình chữ nhật