Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AC=8cm
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: DK=DC
hay ΔDKC cân tại D

a) Xét ΔDAB và ΔDEB có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔDAB=ΔDEB(c-g-c)
Suy ra: DA=DE(Hai cạnh tương ứng)

a, Xét tg ABD và tg EBD có : AB = EB (gt)
gABD = gEBD (BD là tia phân giác của gABE)
BD chung
=> tgABD = tgEBD (c.g.c)
=> DA = DE ( hai cạnh tương ứng )
b,vì tgABD = tgEBD (cmt)
=>gABD = gAEB=90 độ (hai góc tương ứng)
=>gDAK = gDEC = 90 độ
xét tgAKD và tgEDC có: gDAK = gDEC (cmt)
AD = DE ( cmt)
gADK = gEDC ( hai góc đối đỉnh)
=> tgAKD = tgEDC (g.c.g)
=> DK = DC (hai cạnh tương ứng)
=> tg DKC cân tại D
c,xét tgABC vuông tại A ( góc A = 90độ , theo định lí Pytago ta có
BC^2=AB^2 + AC^2
=>AC^2 = 100- 36=64
=> AC = 8 (cm)
a, xét tam giác ABD và tam giác EBD có : BD chung
BA = BE (Gt)
góc ABD = góc EBD do BD là phân giác của góc ABC (gt)
=> tam giác ABD = tam giác EBD (c-g-c)
=> AD = DE (đn)
b, Xét tam giác DCE và tam giác KDA có : AD = DE (Câu a)
góc KDA = góc CDE (đối đỉnh)
góc CED = góc DAK = 90
=> tam giác CE = KA (đn)
có AB = BE (gt)
AB + KA = BK
BE + EC = BC
=> BC = BK
=> BCK cân tại B (đn)
c, dùng ty ta go thôi

a: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
DO đó: ΔADK=ΔEDC
Suy ra: DK=DC
hay ΔDKC cân tạiD
tự vẽ hình giúp mình nha ^^
áp dụng định lí py-ta-go vào tam giác vuông ABC
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC^2=10^2-6^2=100-36=64\)
\(\Rightarrow AC=\sqrt{64}=8\left(cm\right)\)
b) Xét \(\Delta BADvà\Delta BEDcó\)
BD:chung
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
AB=BE(gt)
\(\Delta BAD=\Delta BED\left(c-g-c\right)\)
=>DA=DE
c)Xét \(\Delta KADvà\Delta CEDcó\)
\(\widehat{KAD}=\widehat{CED}\left(=90^0\right)\)
\(\widehat{KDA}=\widehat{CDE}\) (đối đỉnh)
\(=>\Delta KAD=\Delta CED\left(g-c-g\right)\)
=>DC=DK
=> tam giác KDC cân tại D

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: DK=DC
hay ΔDKC cân tại D
c: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
d: Ta có: DK=DC
mà DC>DE
nên DK>DE

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó:ΔADK=ΔEDC
Suy ra:DK=DC
hay ΔDKC cân tại D
c: BC=10cm
AB=6cm
=>AC=8cm

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: ΔABD=ΔEBD
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
Xét ΔDAF và ΔDEC có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
DF=DC
Do đó: ΔDAF=ΔDEC
=>AF=CE
c: Ta có: ΔDAF=ΔDEC
=>\(\widehat{DAF}=\widehat{DEC}\)
mà \(\widehat{DEC}=90^0\)
nên \(\widehat{DAF}=90^0\)
Ta có: \(\widehat{BAD}+\widehat{DAF}=\widehat{BAF}\)
=>\(\widehat{BAF}=90^0+90^0=180^0\)
=>B,A,F thẳng hàng
Xét ΔBFC có BA/AF=BE/EC
nên AE//FC

a, BA = BD (gt)
=> Δ ABD cân tại B (đn)
góc ABC = 60 (gt)
=> Δ ABD đều (dấu hiệu)
b) Ta có\(\widehat{A}\)=90 độ và\(\widehat{B}\)=60 độ =>\(\widehat{C}\)=30 độ (1)
Mà BI là phân giác của \(\widehat{B}\)=> \(\widehat{IBC}\)=30 độ(2)
từ (1) và (2) => Δ IBC cân tại I
c) xét 2 tam giác BIA và BID có: \(\widehat{A}\)+\(\widehat{AIB}\)+\(\widehat{IBA}\)+\(\widehat{IBD}\)+\(\widehat{BDI}\)+\(\widehat{DIB}\)=360 độ
=> \(\widehat{AID}\)=120 độ
=> \(\widehat{DIC}\)=60 độ
Xét Δ BIA và Δ CID có:
DI=AI (Δ BIA=Δ BID)
\(\widehat{BIA}\)=\(\widehat{DIC}\)=60 độ
IB=IC(vìΔ IBC cân)
=>ΔBIA=Δ CID(c.g.c)
=> BA=CD mà BA=BD=> BD=DC
=> D là trung điểm của BC
d) vì AB=\(\dfrac{1}{2}\) BC nên BC=12 cm
Áp dụng định lí py-ta-go ta có:
BC2=AB2+AC2
=> AC2=BC2−AB2
=> AC2=144 - 36=108 cm
=> AC= \(\sqrt{108}\)(cm)
vậy BC=12 cm; AC= \(\sqrt{108}\)cm
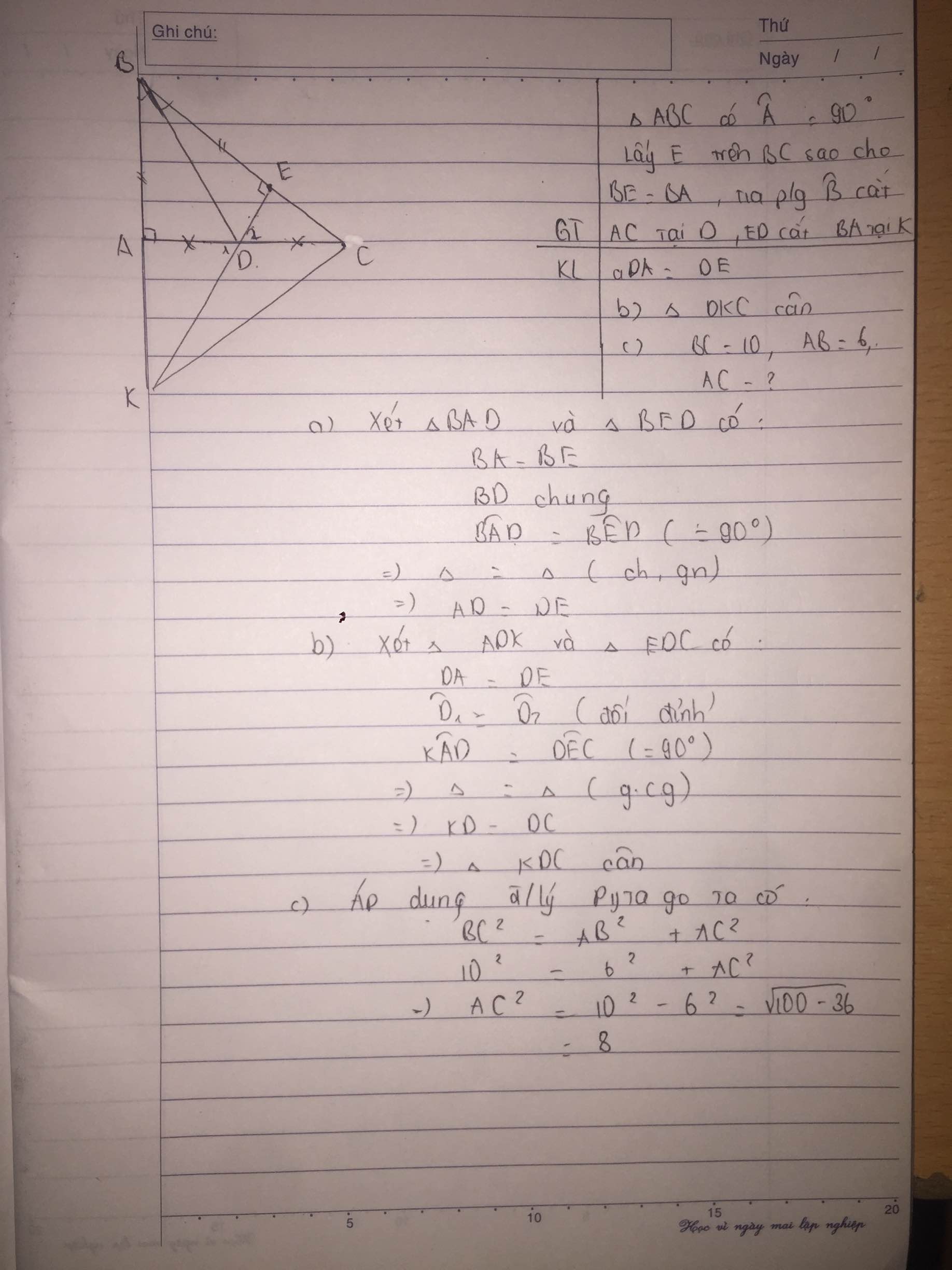
tôi cũg đag cần giải bài này
hình như đề bài sai thì phải