Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có A+B+C=1800
mà A=B+C
suy ra A+B+C=A+A=1800.vậy góc A=900
mà góc BOC=180- (OBC+OCB)
lại có 2(BOC+OCB)=A .vì o là giao điểm của 3 đường phân giác
suy ra BOC+OCB=450.vậy góc BOC bằng 180-45=135

xét tam giác abe va acf
co ;goc f=goc e =90
goc a chung
2 tam giuac dong dang
a) Xét ΔABE và ΔACE có:
\(\widehat{AEB}=\widehat{AFC}\) \(=90^0\)
\(\widehat{CAB}:chung\)
=> ΔABE∼ΔACE (g.g)
b) Xét ΔFHB và ΔEHC có:
\(\widehat{HFB}=\widehat{HEC}\) \(=90^0\)
\(\widehat{FHB}=\widehat{EHC}\) (2 góc đối đỉnh)
=> ΔFHB∼ΔEHC (g.g)
=> \(\frac{HF}{HE}=\frac{HB}{HC}\Leftrightarrow HF.HC=HB.HE\) (đpcm)
c) Theo câu a) ta có: ΔABE∼ΔACF
=> \(\frac{AB}{AC}=\frac{AE}{AF}\)
Xét ΔBAC và ΔEAF có:
\(\widehat{BAC}:chung\)
\(\frac{AB}{AC}=\frac{AE}{AF}\) (cmtrn)
=> ΔBAC∼ΔEAF (c.g.c)
=> \(\widehat{AEF}=\widehat{ABC}\) (2 góc tương ứng)
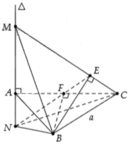
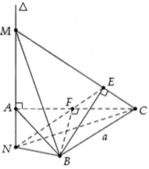
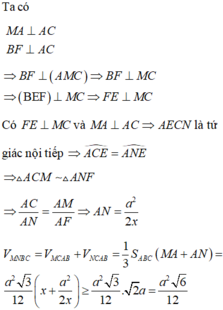
Xét ΔABC có \(\widehat{A}=\widehat{B}+\widehat{C}\)
nên ΔABC vuông tại A
Xét ΔABC có
AO là phân giác
CO là phân giác
Do đó: BO là phân giác của góc CBA
\(\widehat{OCB}+\widehat{OBC}=\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ABC}\right)=\dfrac{1}{2}\cdot90^0=45^0\)
nên \(\widehat{BOC}=135^0\)